2.3 3D游戏所需要的数学知识
2.3.1 向量
向量的加减法遵循平行四边形法则;

可以想象在Unity 中有两个单位向量,分别位于X轴和Y轴上,二者的和、差:

Unity中物体的前后左右上下方向:
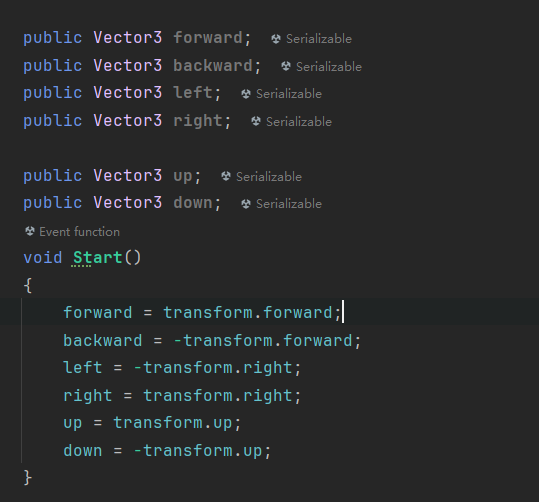
2.3.2 点乘
点乘是向量的数量积、也叫内积(外积是叉乘)。这里我们记住两点就好,(死去的高中知识又来了)
点乘运算:

两向量的点乘结果的正负表示两向量的方向相近程度:(这里两向量均为标量:长度为一的向量)

所以使用点乘可以判断敌人在主角的左前方还是右前方。
例如在推箱子游戏中,判断箱子在主角的方位:
void PushBox(Transform playerTransform, Transform boxTransform){const float ERROR = 0.5f;//箱子正面if (Vector3.Dot(playerTransform.forward, -boxTransform.forward) > ERROR){//省略具体执行代码}else if (Vector3.Dot(playerTransform.forward, boxTransform.forward) >ERROR) //箱子背面{//省略具体执行代码}else if (Vector3.Dot(playerTransform.forward, boxTransform.right) >ERROR) //箱子左边{//省略具体执行代码}else if (Vector3.Dot(playerTransform.forward, -boxTransform.right) >ERROR) //箱子右边{//省略具体执行代码}}
2.3.3 叉乘
叉乘,向量积、外积。两向量的叉乘结果仍旧是向量。结果向量是垂直于两乘数向量所在平面的。

(Unity中的世界坐标系是左手坐标系,所以图示的叉乘结果方向是对应上的)
叉车在shader中有一个经典的运用:法向方向和切线方向的叉乘结果方向为副法线方向;
var bionormal = cross(normal,tangent)
同样我们在Unity可以根据向量的叉乘来判断敌人在主角的左边还是右边;
bool IsEnemyInRight(Transform playerTransform, Transform enemyTransform)
{//Unity中,向量的叉积结果的z轴的正负号可以判断两个向量的相对位置//如果叉积的z轴为正,说明敌人在玩家的右 方var cross = Vector3.Cross(playerTransform.forward, enemyTransform.position - playerTransform.position); return Vector3.Dot(cross, playerTransform.up) > 0;
}
但需要注意,这个做法只存在于默认引力方向的情况下,对于存在改变引力的游戏,还需加入一些额外的逻辑处理。
其实这种方向判断多用在2D游戏中,因为2D仅仅在XOY组成的平面上,可以直接通过简单的叉乘或者点乘来判断一个物体对于另一个物体的方位。在3D空间中的位置关系有多个维度,仅仅通过单一的判断显然不大可能。(左上前方、右下后方等等)
2.3.4 投影
投影跟向量的点乘有点关联,即向量的点乘结果比上一个向量的模便得到另一个向量在本向量上的投影了。

应用:
在固定视角的第三人称游戏中我们需要让主角的移动方向和当前相机方向保持一致,而不是自身的正向方或者正右方。
也就是说视角看向哪里,但是只能在地面上行走(不考虑直升直降 Z轴空间上的移动),所以要把摄像机正前方、右方像投影在XOY平面上,得到真实的可以移动的方向。
void UpdateMove(float speed){var horizontal = Input.GetAxis("Horizontal");var vertical = Input.GetAxis("Vertical");var upAix = Physics.gravity.normalized;//摄像机正前方 在 与重力方向垂直的 XOY平面上的投影var forwardAxis = Vector3.ProjectOnPlane(Camera.main.transform.forward, upAix);//摄像机正右边 在 与重力方向垂直的 XOY平面上的投影var rightAxis = Vector3.ProjectOnPlane(Camera.main.transform.right, upAix);//真正的前行方向var realMoveForwardAxis = (forwardAxis * vertical + rightAxis * horizontal).normalized;//再进行真实的移动transform.position += realMoveForwardAxis * speed * Time.deltaTime;}
2.3.5 四元数
欧拉角旋转会造成万向节死锁问题,所以有关旋转使用最多的是四元数。
通常我们用角-轴 去表示一个物体的旋转。
//将物体绕着自身右轴旋转-90度
transform.rotation = Quaternion.AngleAxis(-90,transform.right);
和欧拉角不同的是四元数可以不断累乘,开发者可以把每一个旋转步骤分开表示并在最终将它们相乘。四元数和矩阵相乘类似,但必须注意相乘的左右顺序:
var rotationA = Quaternion.AngleAxis(35, Vector3.forward);
var rotationB = Quaternion.AngleAxis(45, Vector3.right);
transform.rotation = rotationA * rotationB;
var rotationA = Quaternion.AngleAxis(35, Vector3.forward);var rotationB = Quaternion.AngleAxis(45, Vector3.right);transform.rotation = rotationB * rotationA;

上面两幅图展现出不同的先后旋转顺序对应两种不同的旋转结果;
利用累计乘积可以表示一个转向效果:
private void OnEnable(){//旋转开始方向 终止方向mFromTo = Quaternion.FromToRotation(transform.forward, Vector3.forward);}void Update()
{transform.rotation = Quaternion.Lerp(transform.rotation, mFromTo, 0.1f * Time.deltaTime);
}
FromTo表示对象是从当前Forward方向插值到世界Forward方向,我们将它放到Update里的每一帧去更新。
假如想要知道什么时候插值即将完成,则可以用四元数点乘去判断,它和向量点乘类似,不一样的是其结果会不断接近-1, 1两个零界点,这里用绝对值来进行判断,代码如下:
