Advanced Algorithm —— Hashing and Sketching

Birthday Problem

\(m\) 个人，\(n\) 天，没有两个人生日相同的概率为：

\[\displaystyle{ \begin{align*} \Pr[\mathcal{E}]=\left(1-\frac{1}{n}\right)\cdot \left(1-\frac{2}{n}\right)\cdots \left(1-\frac{m-1}{n}\right) &= \prod_{k=1}^{m-1}\left(1-\frac{k}{n}\right), \end{align*} }\]

当 \(\displaystyle{ m=\sqrt{2n\ln \frac{1}{\epsilon}} }\) ，\(\Pr[\mathcal{E}] \le \epsilon\)。

Universal Hashing

这个定义是对一个 hash 函数族，\(k\) 个不同变量经过这个 hash 后相等的概率不会比随机均匀好。

2-Universal：

考虑对于 \(x_1\neq x_2\)，当 \(\displaystyle{ ((ax_1+b)\bmod p)\bmod M=((ax_2+b)\bmod p)\bmod M }\) 即 \(\displaystyle{ (a(x_1-x_2)\bmod p)\bmod M =0}\)。注意当 \(a\) 取遍 \(1\dots p-1\) 时，\(a(x_1-x_2)\bmod p\) 的值取遍 \(1\dots p-1\)，因此共有 \(\lceil p/M\rceil -1\) 种 \(a\) 会使得 \(a(x_1-x_2)\bmod p\) 为 \(M\) 的倍数。所以：

\[\displaystyle{ \Pr[h(x_1)=h(x_2)]\le \frac{p(p-1)/M}{p(p-1)}=\frac{1}{M}.} \]

Collision number

满足 2-universal hash （\(n\) 个元素映射到 \([M]\) 中）的碰撞数为 \(X\):

\[\displaystyle{ \mathbf{E}[X]=\mathbf{E}\left[\sum_{i\lt j}X_{ij}\right]=\sum_{i\lt j}\mathbf{E}[X_{ij}]=\sum_{i\lt j}\Pr[X_{ij}=1]\le{n\choose 2}\frac{1}{M}\lt \frac{n^2}{2M}. }\]

马尔可夫不等式一下：

\[\displaystyle{ \Pr\left[X\ge \frac{n^2}{2\epsilon M}\right]\le\Pr\left[X\ge \frac{1}{\epsilon}\mathbf{E}[X]\right]\le\epsilon. }\]

Set Membership

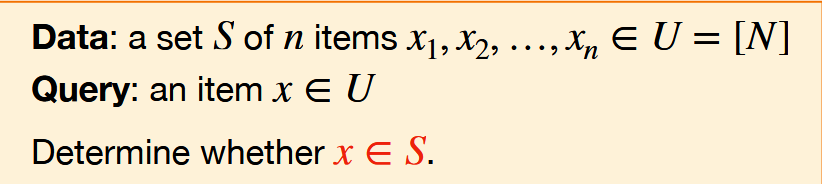
PERFECT HASH：\(h\) 没有碰撞。

由 Collision number 可知，当 \(M=n^2\) 时，有碰撞的概率不超过 \(1/2\)。但是用 \(n^2\) 空间太拉了。

一个更完美的方法是先用一个 hash 函数分成 \(n\) 个桶，每个桶内部使用一个 hash 函数完成 perfect hash，需要空间为桶大小的平方。

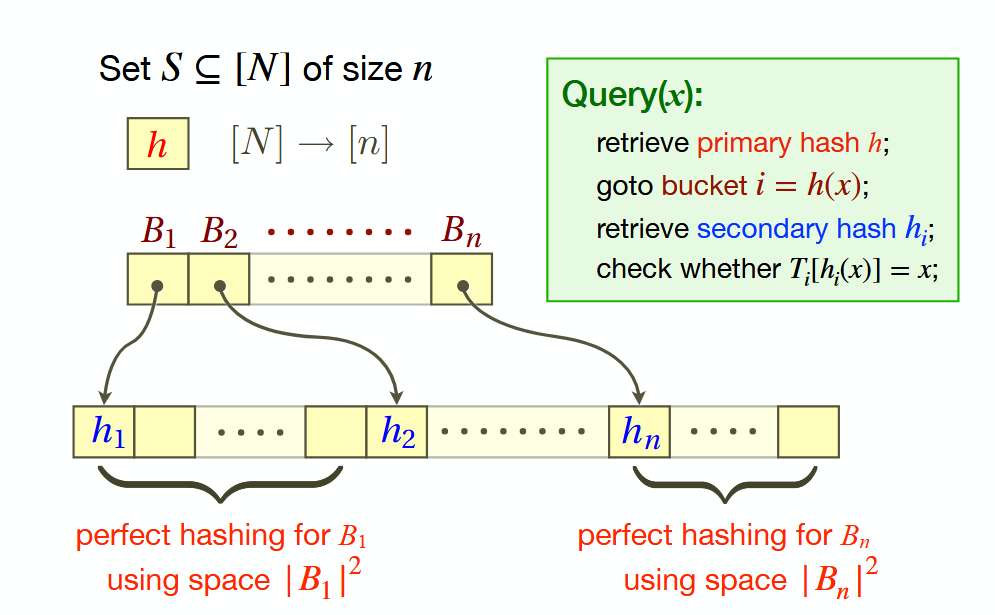
空间分析使用碰撞对数即可。

Bloom filter

\(cn\) 个 bit 以及 \(k\) 个 hash （\([N]\rightarrow [cn]\)）函数：

错误概率，把一个不在 \(S\) 中的判别为在：

\[\displaystyle{ \begin{align*} \Pr[\,\text{wrongly answer ''yes''}\,] &=\Pr[\,\forall 1\le i\le k, A[h_i(x)]=1\,]\\ &=\Pr[\, A[h_1(x)]=1\,]^k=(1-\Pr[\, A[h_1(x)]=0\,])^k\\ &=\left(1-\left(1-\frac{1}{cn}\right)^{kn}\right)^k\\ &\approx \left(1- e^{-k/c}\right)^k \end{align*} }\]

当 \(k=c\ln 2\) 时，这个概率为 \((0.6)^c\)。