减少KVCache

减少KVCache：从MHA，MQA，GQA到MLA

参考链接

科学空间，苏神的blog
大模型推理加速：看图学KVCache

前言

也是终于到了稍微有一点时间的时候，也需要对看过的东西进行简单的总结了。这里就总结一下论文中最喜欢的attention，以及与KVCache之间的关系。

基础：什么是attention？

这一切都要从2017年那一篇 Attention is all you need 开始。为了解决序列预测网络（RNN，包括其代表LSTM，GRU）中无法并行 的问题而被提出。循环神经网络因为新的隐状态 \(h_t\) 取决于前一个状态下的隐状态 \(h_{t-1}\)。因此，为了实现并行化训练，提升训练效率，这篇惊人的文章提出了注意力机制，在捕获序列依赖条件的前提下提供并行计算能力。从此AI的发展一路高歌猛进。几乎快要让像我这样的野狗失业

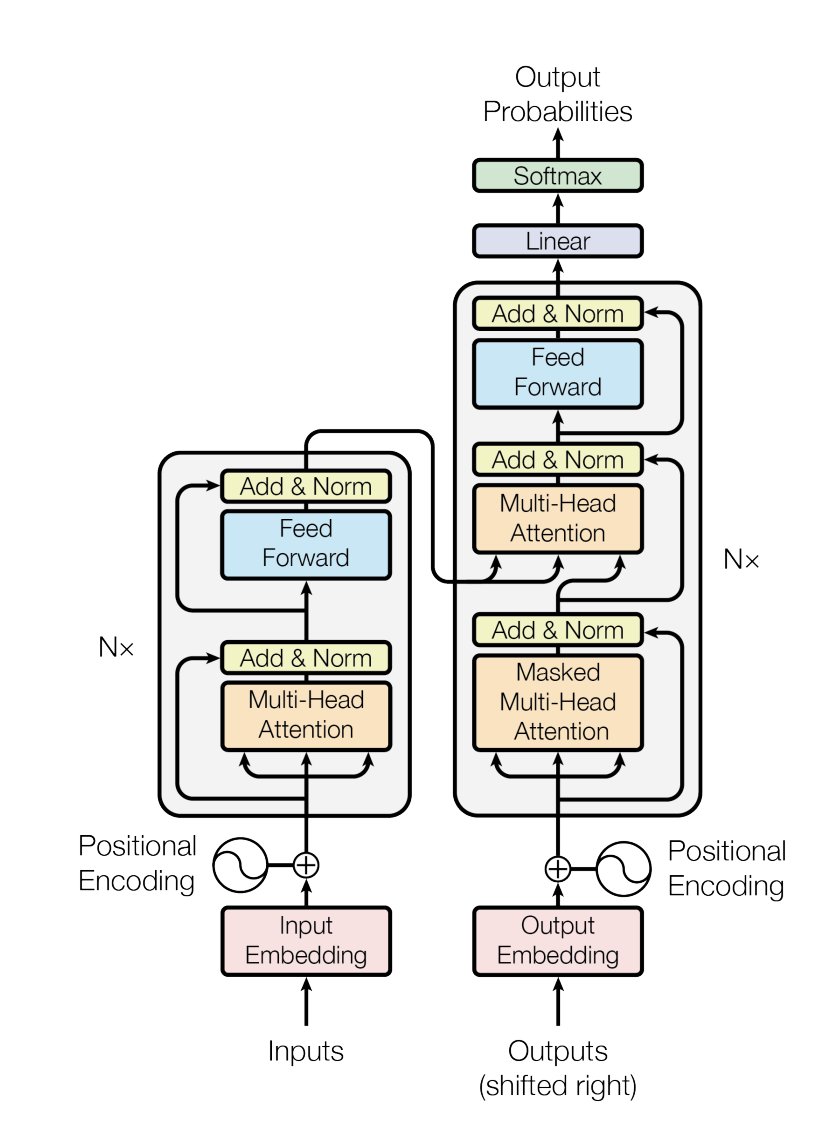
这张图几乎是人尽皆知了。通过位置编码明确序列依赖关系，利用自注意力块（Q，K，V均来自于相同的输入）和交叉注意力块（Q，K来自于输入端，V来自于输出端）来实现序列的预测。

采用缩放点积注意力机制来计算自注意力： \(\textbf{softmax}\left(\dfrac{\mathbf{Q}\mathbf{K}^T}{\sqrt{d_k}}\right)\mathbf{V}\) 来进行计算。（下面这张图也是家喻户晓了，感觉小学生都知道的样子。。。我没在开玩笑）

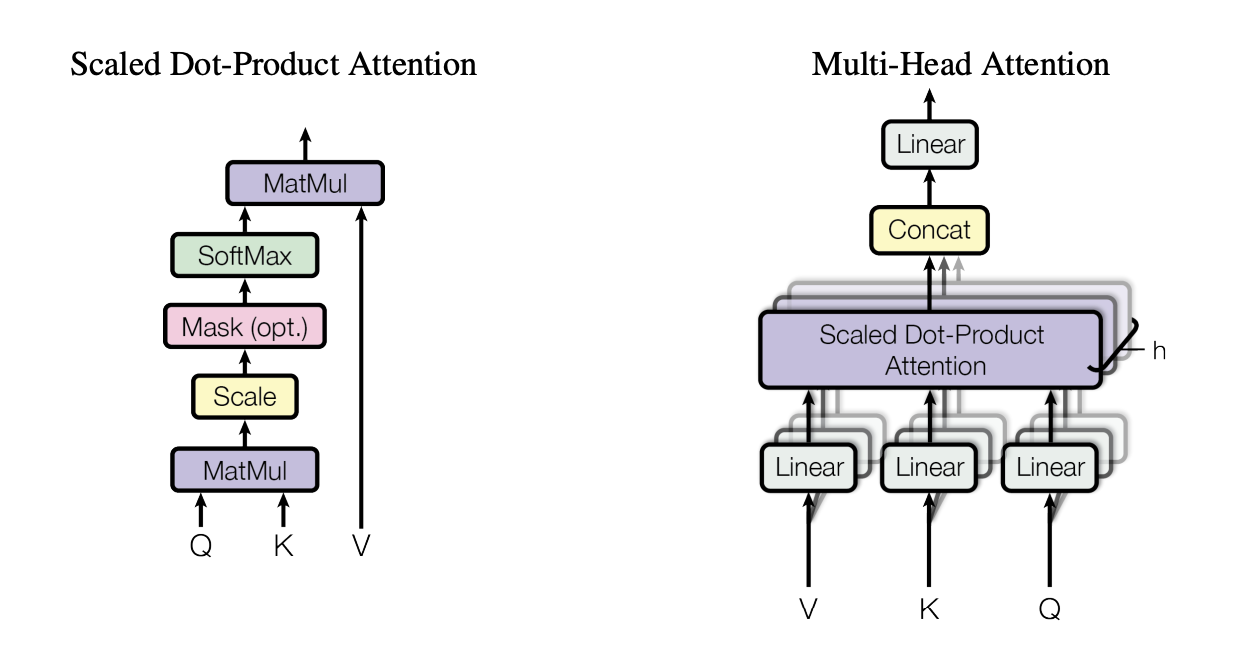
为了提升效率，我们引入投影矩阵，将其映射成 \(d_k, d_k, d_v\) 的向量。并且，为了进一步提升模型的表达能力，我们可以让模型将信息在不同位置通过不同的子空间表示进行投射，也就是多头注意力(MHA) 机制。我们有：

\[\begin{aligned} q_i^{(s)} = x_iW_Q^{(s)}\in\R^{d_k}, W_Q^{(s)}\in\R^{d\times d_k}\\ k_i^{(s)} = x_iW_K^{(s)}\in\R^{d_k}, W_K^{(s)}\in\R^{d\times d_k}\\ v_i^{(s)} = x_iW_V^{(s)}\in\R^{d_v}, W_V^{(s)}\in\R^{d\times d_v} \end{aligned} \]

对于输入 \(x\in\R^d\), 分别进行投影变换。 \((s)\) 代表第 \(s\) 个头的表示。

这样经过缩放点积注意力之后我们就有：

\[\text{MultiHead}(Q,K,V)=\text{Concat}(h_1, \ldots, h_n)W^O \]

也就是每个头自行进行缩放点积注意力后，拼接再投影的结果。

KVCache

接下来我们需要了解KVCache。因为KVCache是后面MQA，GQA，MLA的来源和基础。为什么会具有KVCache这样的东西呢？请看下面的图。

前面我们已经有了：

\[\begin{aligned} q_i^{(s)} = x_iW_Q^{(s)}\in\R^{d_k}, W_Q^{(s)}\in\R^{d\times d_k}\\ k_i^{(s)} = x_iW_K^{(s)}\in\R^{d_k}, W_K^{(s)}\in\R^{d\times d_k}\\ v_i^{(s)} = x_iW_V^{(s)}\in\R^{d_v}, W_V^{(s)}\in\R^{d\times d_v} \end{aligned} \]

在推理场景下（注意训练场景下是不能的，因为训练场景下不是masked output!），我们具有如下的计算图：

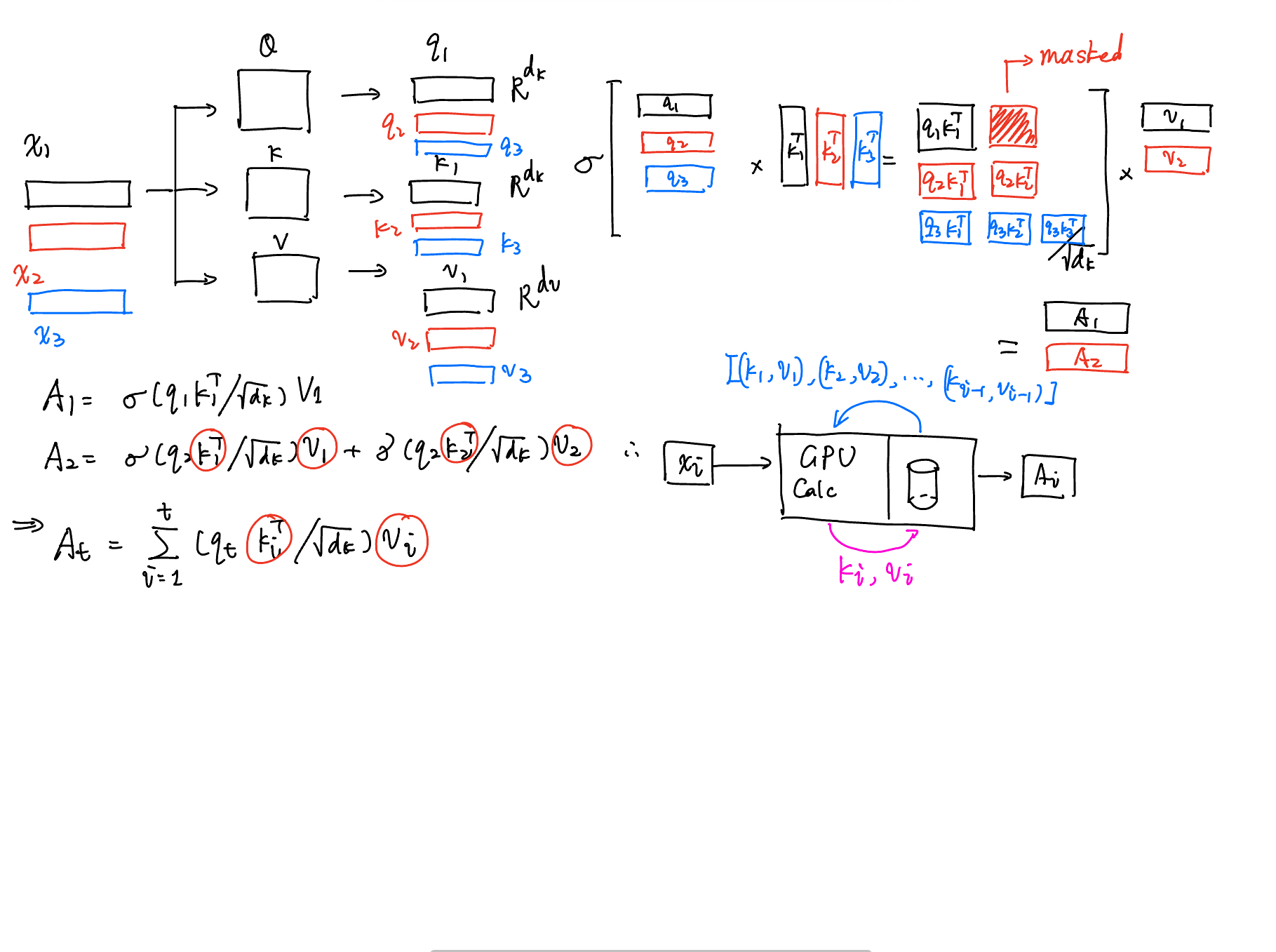
我们发现：我们每次不需要进行重复的计算。我们仅需要：

• 在第\(i\)个输入进入时，计算出其投射 \(q_i, k_i, v_i\)，将 \(k_i, v_i\) 存入显存中，并从显存中取出已经存储的 \(\{(k_1,v_1)\ldots(k_{i-1},v_{i-1})\}\) 使用就好了。
• 并且，我们还可以利用GPU的并行性进行并行计算，最后reduce生成最终结果。

这就是 KVCache 的由来。这样，原先所有的输入序列都需要参与计算，缩小成仅有 新到来的序列 需要参与计算，大大降低了计算复杂度。

MQA

那么，有时候我们的显存实在是不够了（例如，可恶的抠门的实验室要求你必须要用3090甚至是2080跑DeepSeek 7B模型这是太抠门了），我们就必须要学会节省我们的存储。这样，MQA提出的想法就是：每个头共用相同的 \(W_K\) 和 \(W_V\)。这样原先我们需要 \(O(R^{d_k}\times h\times t)\) 存储空间，现在我们只需要存储一个头的 KV 数据。这样就有 \(O(R^{d_k}\times t)\) 了。

GQA

MQA难免会出现表达维度大幅度下降的情况。因此我们就需要增加表达能力。因此，我们可以将头分成多个组来进行注意力机制的计算。这样我们将 \(h\) 个头分成 \(g\) 个组，我们就可以存储 \(O(R^{d_k}\times g\times t)\) 的KV。

MLA

为了增强进一步模型的表达能力，deepseek V3引入了新的多头注意力机制，命名为 多头潜在注意力(multi-latent attention)。其实就是增加了一个投影变换。

我们于是有加入了新的投影变换的公式：

\[\begin{aligned} q_i^{(s)} = x_iW_Q^{(s)}\in\R^{d_k}, W_Q^{(s)}\in\R^{d\times d_k}\\ k_i^{(s)} = c_iW_K^{(s)}\in\R^{d_k}, W_K^{(s)}\in\R^{d_c\times d_k}\\ v_i^{(s)} = c_iW_V^{(s)}\in\R^{d_v}, W_V^{(s)}\in\R^{d_c\times d_v}\\ c_i^{(s)}=x_iW_c^{(s)}\in\R^{d_c},W_c^{(s)}\in\R^{d\times d_c} \end{aligned} \]

但是这样我们不仅引入了新的计算量，甚至存储量还接近于MHA。为了进一步优化我们的KV存储，我们可以观察我们的输出：

\[O_t^{(s)}=\sum\limits_{i=1}^{t}\sigma\left(q_t^{(s)}k_i^{(s)T}/\sqrt{d_k}\right)V_{i}^{(s)} \]

我们发现：在我们的点积部分仅仅和 \(c_i\) 有关：

\[\begin{aligned} q_t^{(s)}k_i^{(s)T}&=(x_iW_Q^{(s)})(W_v^{(s)T}c_i^{T})\\ &=x_i(W_Q^{(s)}W_v^{(s)T})c_i^T \end{aligned} \]

更进一步我们甚至还有：

\[\begin{aligned} O_t^{(s)}&=\sum\limits_{i=1}^{t}\sigma\left(q_t^{(s)}k_i^{(s)T}/\sqrt{d_k}\right)V_{i}^{(s)}\\ &=\sum\limits_{i=1}^{t}\sigma\left(x_i(W_Q^{(s)}W_v^{(s)T})c_i^T/\sqrt{d_k}\right)c_iW_v^{(s)} \end{aligned} \]

这样我们的 KV 都可以替换掉，仅仅存储 \(c_i\) 来实现减少KVCache存储量的效果。

结语

其实优秀的工作就出自于很小很小的点，但是最难能可贵的是能够从这些细小的点中发现他们，改造他们，进行更加完整全面的实验并且介绍他们。这正是野狗窝最欠缺的部分。MHA，MQA，GQA，和MLA都提出了自己减少KVCache的方法，尤其是MLA更是从低秩投影的角度出发（很像LoRA这种通过投影的方式减少时间复杂度），既提升了模型表达维度又减少了KVCache占用，更是让野狗叹为观止。