洛谷 P10936 导弹防御塔 题解

题目描述请移步 https://www.luogu.com.cn/problem/P10936

• 题目简述

有n个防御塔，每个防御塔都有充足的导弹

导弹需要一定时间发出，又需要一定时间冷却

导弹有确定的速度，发出后会沿最短路径攻击任意一个入侵者

有m个入侵者，给定防御塔和入侵者的坐标，求至少多久才能击退所有入侵者

• 解题思路

经过分析，发现直接求最少多久似乎不太可行，于是考虑二分，将问题转化为验证一个时长是否可行

在一定时间内，每个防御塔可以发射固定数量个导弹，这些导弹必须可以击中所有的入侵者，否则不可行

我们可以处理出每个入侵者能被哪些导弹击中（第i个防御塔第1枚，第i个防御塔第2枚...），他必须被其中一枚击中

这有些类似二分图，将入侵者看作一类点，防御塔看作一类点，入侵者与能击中其的导弹连边

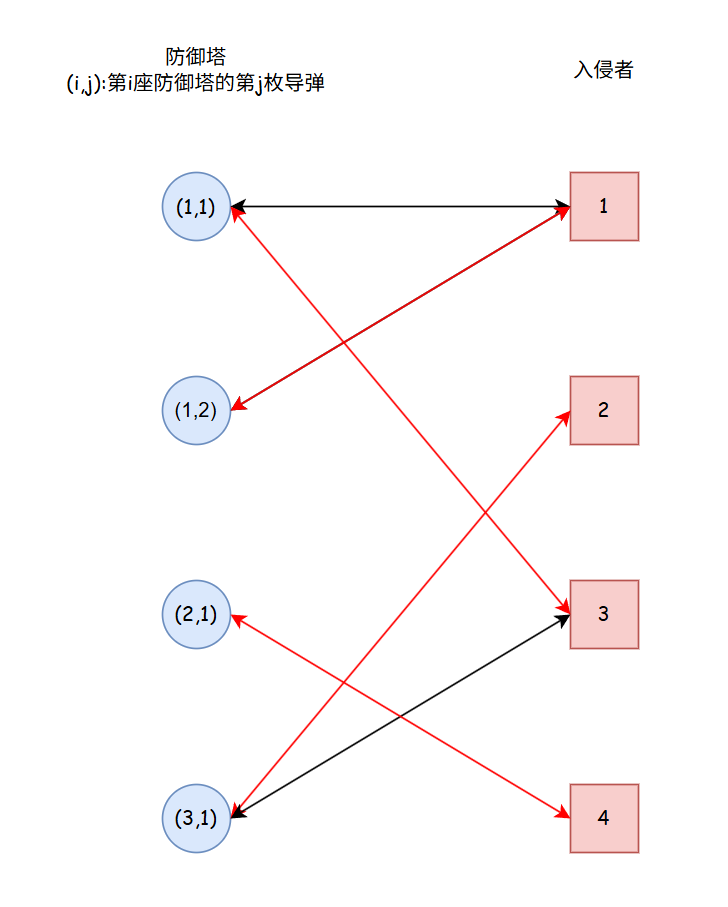
如果最大匹配小于入侵者数量，则不可行；反之，则可行

这样的复杂度或许有些高，但"N,M≤50"的数据还是可以通过的

• 易错点

1. 题目中t1的单位是秒，需先转成分钟

2. 本题许多变量涉及小数，如t1，二分l_r_mid，还有check函数上传的量，注意使用double

3. 先输入的是m个入侵者的坐标，而非n个防御塔

• 代码实现

#include <iostream>
#include <utility>
#include <vector>
#include <cmath>
#include <cstring>
#include <iomanip>
using namespace std;
const int MAX=55;
const int MAXK=2505; 
const double eps=1e-7;//二分精度 
int n,m;
double t1,t2,v;
pair <double,double> a[MAX],b[MAX];
vector <int> edge[MAX];//哪些防御塔能打到这个敌人 
int match[MAXK];//二分图匹配 
bool vis[MAXK];
double dis(int i,int j){//欧几里得距离 return sqrt((a[i].first-b[j].first)*(a[i].first-b[j].first)+(a[i].second-b[j].second)*(a[i].second-b[j].second));
}
bool find(int x){//二分图 for(int j=0;j<edge[x].size();j++){int now=edge[x][j];if(vis[now]==false){vis[now]=true;if(match[now]==0||find(match[now])==true){match[now]=x;return true;}}}return false;
}
bool check(double x){int tot=(x+t2)/(t1+t2);tot=min(tot,m);//总共能发射多少枚导弹 for(int j=1;j<=m;j++){//敌人 edge[j].clear();for(int i=1;i<=n;i++){//防御塔 for(int k=1;k<=tot;k++){if(dis(i,j)/v+k*t1+(k-1)*t2<=x){//可以打到 edge[j].push_back((i-1)*tot+k);} }}}memset(match,0,sizeof(match));for(int i=1;i<=m;i++){memset(vis,0,sizeof(vis));if(find(i)==false){//如果有一个入侵者无法被击退则不可行 return false;}}return true;
} 
int main(){cin>>n>>m>>t1>>t2>>v;t1=t1/60.0;//注意t1单位是秒 for(int i=1;i<=m;i++){cin>>b[i].first>>b[i].second;//入侵者 }for(int i=1;i<=n;i++){cin>>a[i].first>>a[i].second;//防御塔 }double l=0,r=1e9;while(r-l>eps){//小数二分 double mid=(l+r)/2.0;if(check(mid)==true){r=mid;}else{l=mid;}}cout<<fixed<<setprecision(6)<<l;//依据题意保留小数 
}