前题引入
扫描线是用来求给你n个矩阵求他们围起来的总面积。
问题分析
可能有一些弱智的小朋友说直接把所有的矩阵的面积加起来再减掉重复的不就可以啦。
如果,你这么想请问(1<=n<=1e5)请问你该如何应对,所以我们就引入了个新算法:扫描线(废话)
先在我们先画一张图:
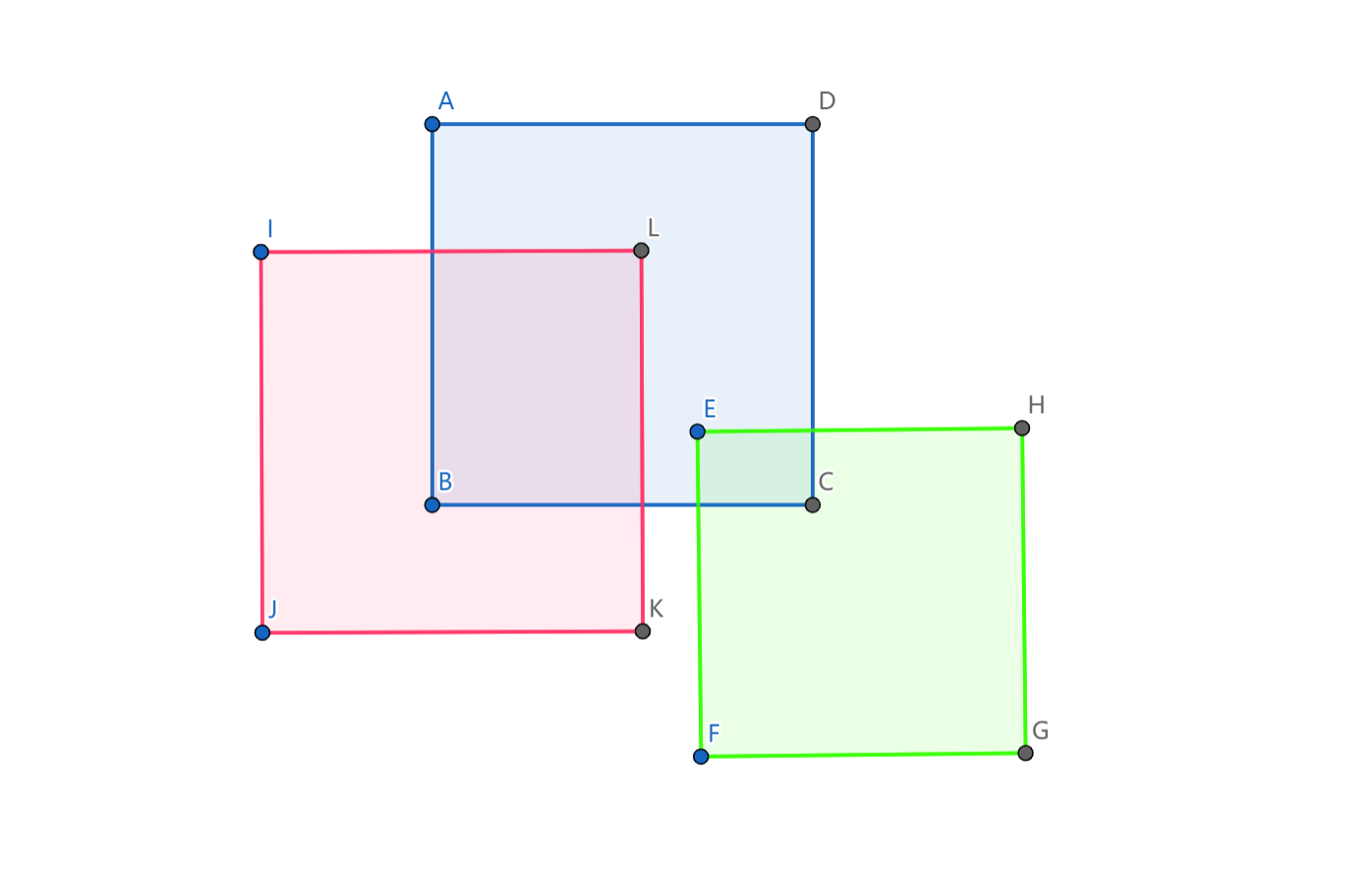
现在有可以用一条直线从左向右或从下往上扫(这里以从下往上为例):
所以我们就可以将这个求所有覆盖面积转化为一个∑截线段长度×扫过的高度,这样是不是简单许多。这就是扫描线的基本原理。
算法实现
问题在于如何才能模拟扫描线从下向上扫过图形,并且快速计算出当前扫描线被截得的长度。
现在假设,扫描线每次会在碰到横边的时候停下来。

简单来说,可对面积可以产生影响的,只是这些横边左右端点的坐标。那么还有一个很严重的问题就是,在某个区间怎么判断这条边还在吗?通过思考可以发现,我们只需要在一个矩形的上下两边加上不同的权值,按照扫描方向,那么下方的边权就是1,上方的边权就是-1,这样子就解决了边的存在问题了
所以我们对每个点按照y升序排序,这样就可以每次先碰到下面,在碰上面了,这里可以对x坐标进行离散化
这里可以用线段树来维护一个当前扫描线的区间复杂度,来优化时间,又不懂线段树的朋友们可前往csdn或OIwiki)进行学习。
算法总结
总之,扫描线大致可以分为2个步骤:
- 初始化,取点存线段,建立线段树
- 扫描每一条“边”
此处附赠理解小视频一枚:

模板P5490
既然看起来如此简单(呃呃呃,是蓝题!),开始实战环节。
戳我看模板
#include<cstdio>
#include<algorithm>
#define ri register int
using namespace std;
typedef long long ll;
ll ans;
ll n;
ll x1,x2,y1,y2;//你知道这里不用万能头吗?doge
ll y[210000];
struct jv{ll y1,y2,x,mark;
}line[210000];
bool cmp(jv a,jv b){return a.x<b.x;}
struct node{ll c,tag;
}tr[810000];
void pushup(ll num,ll l,ll r) {if(!tr[num].tag){if(l==r)tr[num].c=0; else tr[num].c=tr[num<<1].c+tr[num<<1|1].c;}
}
void change(ll num,ll l,ll r,ll y1,ll y2,ll k){//朴素线段树 if(y1<=l&&r<=y2){tr[num].tag+=k;if(tr[num].tag)tr[num].c=y[r+1]-y[l];else tr[num].c=0;pushup(num,l,r);return ;}ll mid=(l+r)>>1;if(y1<=mid)change(num<<1,l,mid,y1,y2,k);if(mid+1<=y2)change(num<<1|1,mid+1,r,y1,y2,k);pushup(num,l,r);
}
int main(){cin>>n; for(ri i=1;i<=n;i++){cin>>x1>>y1>>x2>>y2;y[(i<<1)-1]=y1;y[i<<1]=y2;line[(i<<1)-1]=(jv){y1,y2,x1,3};line[i<<1]=(jv){y1,y2,x2,-3};//记录 } n<<=1; sort(y+1,y+n+1);sort(line+1,line+n+1,cmp);//进行排序 int len=unique(y+1,y+n+1)-(&y[1])-1;for(ri i=1;i<n;i++){y1=lower_bound(y+1,y+len+2,line[i].y1)-y;y2=lower_bound(y+1,y+len+2,line[i].y2)-y-1;//小小的离散化一下 change(1,1,len,y1,y2,line[i].mark);ans+=tr[1].c*(line[i+1].x-line[i].x);//利用公式,加上答案 }cout<<ans; return 0;
}