当前位置： 首页 > news >正文

NOIP 模拟赛十五

news 2025/9/13 22:51:07

range

将所有值以及除以二所能得到的所有值插入一个数据结构里，如果变为 \(0\) 就停止。
那么答案即为第 \(m+1\) 大的值减去第 \(m\) 大的值和前缀最小值取 \(\min\) 的差。
维护这个使用权值树状数组做到小常数 \(O(n\log^2 n)\) 。
注意查排名要跳到 \(< k\) ，然后再 \(+1\) 。

点击查看 

#include <bits/stdc++.h>
#define lep(i, a, b) for (int i = a; i <= b; ++i)
#define rep(i, a, b) for (int i = a; i >= b; --i)
#define il inline
#define cmx(a, b) std::max(a, b)
#define cmn(a, b) std::min(a, b)
#define gmx(a, b) a = cmx(a, b)
#define gmn(a, b) a = cmn(a, b)
#define int long longtemplate <typename T>
void _debug(const T& t) { std::cerr << t << '\n'; }
template <typename T, typename... Args>
void _debug(const T& t, const Args&...res) { std::cerr << t << ' '; _debug(res...); }
#define debug(...) _debug(#__VA_ARGS__ " =", __VA_ARGS__)const int LN = 2e5 + 7;
const int LS = 3e7;
typedef long long ll;
typedef std::pair<int, int> PII;bool FIRPOS;
int n, m, a[LN], V, c[LS], mn, tot;
std::vector <int> op[LN], Ab;
bool ENDPOS;il int id(int x) { return std::lower_bound(Ab.begin(), Ab.end(), x) - Ab.begin() + 1; }
il void ins(int x) { ++tot, x = V - x + 1; while (x <= V) ++c[x], x += x & -x; }
il int kth(int k) {int s = 0; gmn(k, tot);rep(i, 25, 0) if (s + (1 << i) <= V and c[s + (1 << i)] < k) s += (1 << i), k -= c[s];return V - s;
}
il int qry() { return Ab[kth(m + 1) - 1] - cmn(Ab[kth(m) - 1] / 2, mn); }signed main() {std::ios::sync_with_stdio(false),std::cin.tie(nullptr), std::cout.tie(nullptr);int c1 = clock(); int x;std::cin >> n >> m;lep(i, 1, n) {std::cin >> a[i]; x = a[i];op[i].emplace_back(x);while (true) { op[i].emplace_back(x /= 2); if (!x) break; }for (int v : op[i]) Ab.emplace_back(v);}std::sort(Ab.begin(), Ab.end()), Ab.erase(std::unique(Ab.begin(), Ab.end()), Ab.end()); V = Ab.size();mn = INT_MAX;lep(i, 1, n) { gmn(mn, a[i]);for (int v : op[i]) ins(id(v));std::cout << qry() << ' ';}std::cout << '\n';#ifdef DEBUGstd::cerr << clock() - c1 << " ms " << fabs(&ENDPOS - &FIRPOS) / 1024 / 1024 << " MB\n";
#endifreturn 0;
}

sequence

题目即为有多少种覆盖方案合法。
如果后 \(k\) 个那些覆盖到前 \(n-k\) 个是确定的，那么只存在一种对应方案使他们合法，于是我们只关心有哪些向前覆盖。
在值域考虑，只要覆盖就向其连边，最后会变成若干个环和若干个链。
每一条链的链尾就对应这 \(n-k\) 中哪些被覆盖，被覆盖的一定是值域的后缀，因为后面一定更大。
对于有 \(i\) 条链的情况，答案即为 \({k\choose i}\times (n-k)^{\underline{n-k-i}}\) 。
含义：确定哪些作为链尾的上一段，剩下的可以随便连（保证每个点的入度 \(\le 1\)）

那么哪些 \(i\) 是能够造成贡献的呢？
发现一定是一个后缀，也就是 \([i', n-k]\) ，设 \(p_i=b_i^{-1}\) 。
则 \(i'=\min_{[p_i>p_{i+1}]} i\) ，即最长上升子序列的末尾值中可能的最小值。

使用堆搭配惰性删除动态维护 \(i'\) 即可。

点击查看代码 

#include <bits/stdc++.h>
#define lep(i, a, b) for (int i = a; i <= b; ++i)
#define rep(i, a, b) for (int i = a; i >= b; --i)
#define il inline
#define cmx(a, b) std::max(a, b)
#define cmn(a, b) std::min(a, b)
#define gmx(a, b) a = cmx(a, b)
#define gmn(a, b) a = cmn(a, b)template <typename T>
void _debug(const T& t) { std::cerr << t << '\n'; }
template <typename T, typename... Args>
void _debug(const T& t, const Args&...res) { std::cerr << t << ' '; _debug(res...); }
#define debug(...) _debug(#__VA_ARGS__ " =", __VA_ARGS__)const int LN = 5e5 + 7;
const int mod = 998244353;
typedef long long ll;
typedef std::pair<int, int> PII;bool FIRPOS;int m, n, b[LN], k, fac[LN], inv[LN], pos[LN], p, sum[LN];
std::priority_queue <int, std::vector<int>, std::greater<int> > q; bool del[LN];bool ENDPOS;il int add(int u, int v) { return u + v >= mod ? u + v - mod : u + v; }
il void upa(int& u, int v) { u = add(u, v); }
il int mul(ll u, ll v) { return u * v >= mod ? u * v % mod : u * v; }
il void upm(int& u, int v) { u = mul(u, v); }
il int MyPow(int a, int b) { int ans = 1; for (; b; b >>= 1, upm(a, a)) if (b & 1) upm(ans, a); return ans; }
il int C(int n, int m) { if (n < 0 or m < 0 or n < m) return 0; return mul(mul(fac[n], inv[m]), inv[n - m]); }
il void lig(int u) { del[u] = false, q.push(u); }
il void ext(int u) { del[u] = true; }
il void ck(int x) {if (x < 1 or x > n - k) return;if (pos[x] > pos[x + 1]) lig(x);else ext(x);
}
il int qry() {while (del[q.top()]) q.pop();return n - k - q.top();
}int main() {std::ios::sync_with_stdio(false),std::cin.tie(nullptr), std::cout.tie(nullptr);int c1 = clock();int x, y;fac[0] = 1;lep(i, 1, LN - 1) fac[i] = mul(fac[i - 1], i);inv[LN - 1] = MyPow(fac[LN - 1], mod - 2);rep(i, LN - 1, 1) inv[i - 1] = mul(inv[i], i);std::cin >> n >> k >> m;lep(i, 1, n - k) std::cin >> b[i], pos[b[i]] = i, del[i] = true;lep(i, 1, n - k) ck(i);rep(i, n - k, 0) sum[i] = add(sum[i + 1], mul(C(k, i), mul(fac[k], inv[i])));std::cout << sum[qry()] << '\n';while (m--) {std::cin >> x >> y;std::swap(b[x], b[y]), pos[b[x]] = x, pos[b[y]] = y;ck(b[x] - 1), ck(b[x]), ck(b[y] - 1), ck(b[y]);std::cout << sum[qry()] << '\n';}
#ifdef DEBUGstd::cerr << clock() - c1 << " ms " << fabs(&ENDPOS - &FIRPOS) / 1024 / 1024 << " MB\n";
#endifreturn 0;
}

tour

首先考虑 type = 1 ，将关键点按照 \(x+y\) 排序，根据对角线顺序来 \(dp\) 。
设 \(f[a, b]\) 为第一人走到 \(a\) ，第二人走到 \(b\) 的方案数。
转移到 \(f[a, i]\) 或 \(f[i, b]\) ，要求 \(i=a+1\) 或 \(i=b+1\) 。

直接 \(dp\) 会有一个问题：

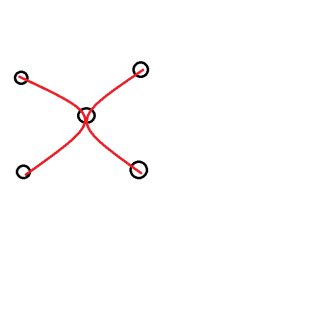
这条路径会被算到多次，原因在于我们在转移过程中无法保证不经过其他的关键点。
我们考虑容斥，对于两点之间的路径，我们钦定同时经过 \(S\) 中的关键点。
则一个其他关键点都不经过的方案即为 \(\sum_S (-1)^{\left|S\right|} f(S)\) ，我们直接将容斥系数融入 \(dp\) 过程。
每钦定一个关键点同时经过，它的所有转移同时乘上 \(-1\) 即可。
初值应设为 \(-1\) ，因为钦定了初始点重合。

对于 type = 2 ，我们将 \(A=(1, 2), B=(2, 1), C=(n-1, m), D=(n, m - 1)\) 加入关键点。
然后 f[A][B] = 1 ，按照如上 \(dp\) ，\(ans=2\times(f[C][D] - f[D][C])\) 。

下面来叙述这样为什么是对的，可以发现这是 \(LGV\) 引理 \(n=2\) 的特殊情况。
每一对 (\(A\rightarrow C ,B\rightarrow D)\) 中途如果有交点，取第一个交点交换路径，一定与一对 \((A\rightarrow D,B\rightarrow C )\) 构成双射。

点击查看 

#include <bits/stdc++.h>
#define lep(i, a, b) for (int i = a; i <= b; ++i)
#define rep(i, a, b) for (int i = a; i >= b; --i)
#define il inline
#define cmx(a, b) std::max(a, b)
#define cmn(a, b) std::min(a, b)
#define gmx(a, b) a = cmx(a, b)
#define gmn(a, b) a = cmn(a, b)template <typename T>
void _debug(const T& t) { std::cerr << t << '\n'; }
template <typename T, typename... Args>
void _debug(const T& t, const Args&...res) { std::cerr << t << ' '; _debug(res...); }
#define debug(...) _debug(#__VA_ARGS__ " =", __VA_ARGS__)const int LN = 2e6 + 7;
const int LK = 5000 + 7;
const int mod = 998244353;
typedef long long ll;
typedef std::pair<int, int> PII;bool FIRPOS;int type, m, n, k, fac[LN], inv[LN];
PII a[LK]; int f[LK][LK], to[LK][LK];bool ENDPOS;il int add(int u, int v) { return u + v >= mod ? u + v - mod : u + v; }
il void upa(int& u, int v) { u = add(u, v); }
il int mul(ll u, ll v) { return u * v >= mod ? u * v % mod : u * v; }
il void upm(int& u, int v) { u = mul(u, v); }
il int MyPow(int a, int b) { int ans = 1; for (; b; b >>= 1, upm(a, a)) if (b & 1) upm(ans, a); return ans; }
il int C(int n, int m) { if (n < 0 or m < 0 or n < m) return 0; return mul(mul(fac[n], inv[m]), inv[n - m]); }
il int trn(int xa, int ya, int xb, int yb) { return C(xb - xa + yb - ya, xb - xa); }
void solve1() {std::memset(f, 0, sizeof(f));f[1][1] = mod - 1;lep(i, 2, k) {lep(j, 1, i - 2) {upa(f[i][i - 1], mul(f[j][i - 1], to[j][i])), upa(f[i - 1][i], mul(f[i - 1][j], to[j][i]));upa(f[j][i], mul(f[j][i - 1], to[i - 1][i])), upa(f[i][j], mul(f[i - 1][j], to[i - 1][i]));upa(f[i][i], mod - mul(add(f[i - 1][j], f[j][i - 1]), mul(to[i - 1][i], to[j][i])));}upa(f[i][i - 1], mul(f[i - 1][i - 1], to[i - 1][i])), upa(f[i - 1][i], mul(f[i - 1][i - 1], to[i - 1][i]));upa(f[i][i], mod - mul(f[i - 1][i - 1], mul(to[i - 1][i], to[i - 1][i])));}
}
void solve2() {std::memset(f, 0, sizeof(f));f[1][2] = 1;lep(i, 3, k) lep(j, 1, i - 1) {upa(f[i][i - 1], mul(f[j][i - 1], to[j][i])), upa(f[i - 1][i], mul(f[i - 1][j], to[j][i]));upa(f[j][i], mul(f[j][i - 1], to[i - 1][i])), upa(f[i][j], mul(f[i - 1][j], to[i - 1][i]));}
}int main() {std::ios::sync_with_stdio(false),std::cin.tie(nullptr), std::cout.tie(nullptr);int c1 = clock();fac[0] = 1;lep(i, 1, LN - 1) fac[i] = mul(fac[i - 1], i);inv[LN - 1] = MyPow(fac[LN - 1], mod - 2);rep(i, LN - 1, 1) inv[i - 1] = mul(inv[i], i);std::cin >> type >> n >> m >> k; ++k;lep(i, 2, k) {std::cin >> a[i].first >> a[i].second;if (a[i].first == 1 and a[i].second == 1) --i, --k;if (a[i].first == n and a[i].second == m) --i, --k;}int ans1, ans2;a[1] = { 1, 1 }, a[++k] = { n, m };lep(i, 1, k) lep(j, i + 1, k) to[i][j] = trn(a[i].first, a[i].second, a[j].first, a[j].second);solve1(), ans1 = f[k][k];a[1] = { 1, 2 }, a[k] = { 2, 1 }, a[++k] = { n, m - 1 }, a[++k] = { n - 1, m };std::sort(a + 1, a + 1 + k), k = std::unique(a + 1, a + 1 + k) - a - 1;std::sort(a + 1, a + 1 + k, [](const PII& x, const PII& y){ return x.first + x.second != y.first + y.second ? x.first + x.second < y.first + y.second : x.second < y.second; });lep(i, 1, k) lep(j, i + 1, k) to[i][j] = trn(a[i].first, a[i].second, a[j].first, a[j].second);solve2(), ans2 = add(f[k - 1][k], mod - f[k][k - 1]);upm(ans2, 2);if (type != 2) std::cout << ans1 << '\n';if (type != 1) std::cout << ans2 << '\n';#ifdef DEBUGstd::cerr << clock() - c1 << " ms " << fabs(&ENDPOS - &FIRPOS) / 1024 / 1024 << " MB\n";
#endifreturn 0;
}

query

每 \(\sqrt n\) 个操作为一组，对于一组内的操作，按顺序维护块。
翻转即将某些块裂开，然后给一些块打标记，询问同理，打上询问标记。

然后我们就维护了 \(O(\sqrt n)\) 个块，每个块存储了其贡献给了哪些询问。
枚举答案，对于那些目前没有答案且贡献给其的块内都没有当前答案值时，更新其答案为当前枚举量。

使用 bitset 维护上述过程。

具体的细节上，我们使用链表维护块的分类和打标记，枚举答案时我们提前存下每个值出现在哪些块里即可。
每处理完一组都重构当前序列。

复杂度 \(O(q\sqrt n + \frac{n^2}{w})\) 。

点击查看 

#include <bits/stdc++.h>
#define lep(i, a, b) for (int i = a; i <= b; ++i)
#define rep(i, a, b) for (int i = a; i >= b; --i)
#define il inline
#define cmx(a, b) std::max(a, b)
#define cmn(a, b) std::min(a, b)
#define gmx(a, b) a = cmx(a, b)
#define gmn(a, b) a = cmn(a, b)template <typename T>
void _debug(const T& t) { std::cerr << t << '\n'; }
template <typename T, typename... Args>
void _debug(const T& t, const Args&...res) { std::cerr << t << ' '; _debug(res...); }
#define debug(...) _debug(#__VA_ARGS__ " =", __VA_ARGS__)const int LN = 2e5 + 7;
const int LQ = 484;
const int B = LQ - 1;
typedef long long ll;
typedef std::bitset <LQ> Bit;
typedef std::pair<int, int> PII;bool FIRPOS;struct list {int pre, suf, l, r; Bit qy;list() { qy.reset(), l = 0, pre = suf = r = -1; }
}lis[LN]; int st, ed = 1, liscnt = 1;
int op[LN], x[LN], y[LN], qry;
std::bitset <LN> vis;
std::vector <int> pos[LN];int n, m, a[LN], b[LN], ans[LN];bool ENDPOS;il int ABS(int x) { return x > 0 ? x : -x; }
il void ins(int x, int y) {lis[lis[x].suf].pre = y, lis[y].suf = lis[x].suf;lis[x].suf = y, lis[y].pre = x;
}
il int len(int x) { return ABS(lis[x].r - lis[x].l) + 1; }
il int rub() { int p = ++liscnt; lis[p] = list(); return p; }
void slk(int x, int k) {if (len(x) == k or !k) return;int y = rub(); lis[y].qy = lis[x].qy;if (lis[x].l <= lis[x].r)lis[y].r = lis[x].r, lis[y].l = lis[x].l + k, lis[x].r = lis[x].l + k - 1;else lis[y].r = lis[x].r, lis[y].l = lis[x].l - k, lis[x].r = lis[x].l - k + 1;ins(x, y);
}
il void init() {lep(i, 0, n) pos[i].clear();lep(i, 1, n) pos[a[i]].emplace_back(i);lis[st].suf = ed, lis[ed].pre = st, liscnt = 1;ins(st, rub()), lis[liscnt].l = 1, lis[liscnt].r = n;
}
void reform() { int x = lis[st].suf, len = 0;while (x != ed) {if (lis[x].l <= lis[x].r) lep(i, lis[x].l, lis[x].r) b[++len] = a[i];else rep(i, lis[x].l, lis[x].r) b[++len] = a[i]; x = lis[x].suf;}lep(i, 1, n) a[i] = b[i];init();
}
void rev(int l, int r) { int x = lis[st].suf, LEN = 0, L = st, R = ed; --l;while (x != ed) {if (LEN < l and l <= LEN + len(x)) slk(x, l - LEN), L = x;if (LEN < r and r <= LEN + len(x)) slk(x, r - LEN), R = lis[x].suf;LEN += len(x), x = lis[x].suf;} int fro = L, nxt;x = lis[R].pre;while (x != L) {nxt = lis[x].pre, lis[x].pre = fro, lis[fro].suf = x;std::swap(lis[x].l, lis[x].r), fro = x, x = nxt;}x = fro, lis[x].suf = R, lis[R].pre = x;
}
void cov(int l, int r, int k) { int x = lis[st].suf, LEN = 0, L = st, R = ed; --l;while (x != ed) {if (LEN < l and l <= LEN + len(x)) slk(x, l - LEN), L = x;if (LEN < r and r <= LEN + len(x)) slk(x, r - LEN), R = lis[x].suf;LEN += len(x), x = lis[x].suf;}x = lis[L].suf;while (x != R) lis[x].qy.set(k), x = lis[x].suf;
}
void solve() { int tot = 0;lep(i, 1, qry) {if (op[i] == 1) rev(x[i], y[i]);else cov(x[i], y[i], tot++);}int x = lis[st].suf;while (x != ed) {if (lis[x].l <= lis[x].r) lep(i, lis[x].l, lis[x].r) b[i] = x;else rep(i, lis[x].l, lis[x].r) b[i] = x; x = lis[x].suf;}Bit U, A, C; int cnt = 0;lep(i, 0, tot - 1) U.set(i);lep(i, 0, n + 1) { C = A;for (auto p : pos[i]) C |= lis[b[p]].qy;C = ~C & U, A |= C;while (C.any()) x = C._Find_first(), ans[x] = i, C.reset(x), ++cnt;if (cnt == tot) break;}lep(i, 0, tot - 1) std::cout << ans[i] << '\n'; qry = 0;reform();
}int main() {std::ios::sync_with_stdio(false),std::cin.tie(nullptr), std::cout.tie(nullptr);int c1 = clock();std::cin >> n >> m; int qk = 0;lep(i, 1, n) {std::cin >> a[i];if (!vis[a[i]]) vis.set(a[i]), ++qk;} init(); int tot = 0;qk = (qk > n / 2);lep(i, 1, m) { ++qry;std::cin >> op[qry] >> x[qry] >> y[qry]; tot += (op[qry] > qk);if (i == m or tot == B) solve(), tot = 0;}#ifdef DEBUGstd::cerr << clock() - c1 << " ms " << fabs(&ENDPOS - &FIRPOS) / 1024 / 1024 << " MB\n";
#endifreturn 0;
}
http://www.wxhsa.cn/company.asp?id=3114

相关文章：

  • 面试必备进程调度：fg,bg,jobs,ctrl+z,
  • 完整教程：计算机毕设 java 多媒体教室管理系统 基于 Java+SSM 的多媒体教室运维平台 Java+MySQL 的教室预约与设备管理系统
  • 笔记一
  • 二十、指令流水线的基本实现
  • 物料模板匹配成功后，自动跟随的逻辑
  • TCL t508n 关闭电话语音王提醒/改用4G
  • 完整教程：Markdown 编辑器 语法
  • 天地图的带洞多边形操作
  • k8s集群中一台etcd的pod异常
  • 深入解析：基于51单片机电子称称重压力检测阈值报警系统设计
  • 手撕大模型｜KVCache 原理及代码解析
  • Kuby免疫学读书笔记01——造血干细胞
  • 微信群机器人开发
  • 动态规划和马尔可夫决策对比
  • 20250913 之所思 - 人生如梦
  • 动态规划
  • 电视剧和综艺
  • 天地图编辑多边形和折线时，双击删除编辑点
  • POCamp 2023
  • 美团AI面试
  • 技术面：Spring (bean的生命周期、创建方式、注入方式、作用域)
  • 马尔可夫决策
  • 十九、指令流水线的基本概念
  • 本地布署Diffusers库 实现文生图 - yi
  • 【光照】[光照模型]发展里程碑时间线
  • 算法设计作业-week1
  • git merge
  • C语言学习
  • Ubuntu 的剪贴板
  • IDAPro--MCP详细配置教程