CF819B Mister B and PR Shifts
题目描述
Some time ago Mister B detected a strange signal from the space, which he started to study.
After some transformation the signal turned out to be a permutation $ p $ of length $ n $ or its cyclic shift. For the further investigation Mister B need some basis, that's why he decided to choose cyclic shift of this permutation which has the minimum possible deviation.
Let's define the deviation of a permutation $ p $ as 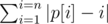 .
.
Find a cyclic shift of permutation $ p $ with minimum possible deviation. If there are multiple solutions, print any of them.
Let's denote id $ k $ ( $ 0<=k<n $ ) of a cyclic shift of permutation $ p $ as the number of right shifts needed to reach this shift, for example:
- $ k=0 $ : shift $ p_{1},p_{2},...\ p_{n} $ ,
- $ k=1 $ : shift $ p_{n},p_{1},...\ p_{n-1} $ ,
- ...,
- $ k=n-1 $ : shift $ p_{2},p_{3},...\ p_{n},p_{1} $ .
输入格式
First line contains single integer $ n $ ( $ 2<=n<=10^{6} $ ) — the length of the permutation.
The second line contains $ n $ space-separated integers $ p_{1},p_{2},...,p_{n} $ ( $ 1<=p_{i}<=n $ ) — the elements of the permutation. It is guaranteed that all elements are distinct.
输出格式
Print two integers: the minimum deviation of cyclic shifts of permutation $ p $ and the id of such shift. If there are multiple solutions, print any of them.
输入输出样例 #1
输入 #1
3
1 2 3
输出 #1
0 0
输入输出样例 #2
输入 #2
3
2 3 1
输出 #2
0 1
输入输出样例 #3
输入 #3
3
3 2 1
输出 #3
2 1
说明/提示
In the first sample test the given permutation $ p $ is the identity permutation, that's why its deviation equals to $ 0 $ , the shift id equals to $ 0 $ as well.
In the second sample test the deviation of $ p $ equals to $ 4 $ , the deviation of the $ 1 $ -st cyclic shift $ (1,2,3) $ equals to $ 0 $ , the deviation of the $ 2 $ -nd cyclic shift $ (3,1,2) $ equals to $ 4 $ , the optimal is the $ 1 $ -st cyclic shift.
In the third sample test the deviation of $ p $ equals to $ 4 $ , the deviation of the $ 1 $ -st cyclic shift $ (1,3,2) $ equals to $ 2 $ , the deviation of the $ 2 $ -nd cyclic shift $ (2,1,3) $ also equals to $ 2 $ , so the optimal are both $ 1 $ -st and $ 2 $ -nd cyclic shifts.
解题报告
这里其实有个小小的套路:看到绝对值,一般都要按正负数进行分类讨论。
先说一下,这题作者是在本校的小测中的写的,在小测中本题被改成了左移,所以以下的讨论是对于左移而言的,最后再用对称性转换回来。
现在考虑已经进行了 \(k-1\) 次左移,正在进行第 \(k\) 次左移。
若不考虑绝对值,除了第一项,每一个 \(p_i\) 的贡献会从 \(p_i-i\) 变到 \(p_i-(i-1)\),而第一项 \(p_1\) 的贡献会从 \(p_1-1\) 变为 \(p_1-n\)。
现在加上绝对值,进行分类讨论:
- 第一项比较特殊,我们单独考虑其变化,就是 \(|p_1-n|-|p_1-1|\)。
- 当 \(i\neq 1\),如果 \(p_i-i < 0\),那么 \(|p_i-(i-1)|-|p_i-i|=-1\)。
- 当 \(i\neq 1\),如果 \(p_i-i \geq 0\),那么 \(|p_i-(i-1)|-|p_i-i|=1\)。
那么设第 \(k\) 次左移后的 \(\sum_{i=1}^{n} |p_i-i|\) 为 \(ans_{k}\),左移前的 \(p_i-i < 0\) 的个数为 \(cnt_1\),\(p_i-i \geq 0\) 的个数为 \(cnt_2\),那么就有以下递推关系:
这里行末的 \(+1\) 是因为肯定有 \(p_1-1\geq0\),那么它会包含进 \(cnt_2\),所以会多个 \(+1\),需要减回来。
那么现在的问题就是正确维护每一次左移前的 \(cnt_1\) 和 \(cnt_2\)。考虑对原数列进行了第 \(k\) 次左移和第 \(k-1\) 次左移负数和正数的个数的变化,那么:
- 对于每个 \(p_i\),在第 \(i\) 次时会被移到最后,若 \(p_i \neq n\),肯定有 \(p_i-1\geq0\) 且 \(p_i-n < 0\)。
- 如果 \(p_i \leq i\),若 \(p_i \neq n\),在第 \(i-p_i\) 次时会变成正数。
- 如果 \(p_i > i\),若 \(p_i \neq n\),在第 \(i\) 次时会被移到最后,然后再左移第 \(n-p_i\) 次时会变成正数。
- 如果 \(p_i=n\),一直有 \(p_i-i \geq 0\)。
这样就可以正确维护了,同时 \(k\) 次左移相当于 \(n-k\) 次右移。
复杂度 \(O(n)\),代码如下:
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int INF=0x3f3f3f3f;
const int N=2001100;#define ckmax(x,y) ( x=max(x,y) )
#define ckmin(x,y) ( x=min(x,y) )inline int read()
{int f=1,x=0; char ch=getchar();while(!isdigit(ch)) { if(ch=='-') f=-1; ch=getchar(); }while(isdigit(ch)) { x=x*10+ch-'0'; ch=getchar(); }return f*x;
}int n;
int w[N<<1];
int d[N][2];inline void debug()
{for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){int pos=i-j+1;if(pos<=0) pos+=n;cout<<w[i]-pos<<" ";}cout<<endl;}
}signed main()
{n=read();for(int i=1;i<=n;i++)w[i+n]=w[i]=read();int ans=0,tmp=0,K=n;for(int i=1;i<=n;i++){d[i][0]++,d[i][1]--;if(w[i]>i) d[i+n-w[i]][0]--,d[i+n-w[i]][1]++;else d[i-w[i]][0]--,d[i-w[i]][1]++;}int cnt1=0,cnt2=0;for(int i=1;i<=n;i++){ans+=abs(w[i]-i);cnt1+=w[i]<i;cnt2+=w[i]>=i;}tmp=ans;for(int i=1;i<n;i++){tmp-=abs(w[i]-1)-abs(w[i]-n);tmp-=cnt1,tmp+=cnt2,tmp--;cnt1+=d[i][0],cnt2+=d[i][1];if(tmp<ans) K=i;ckmin(ans,tmp);}printf("%lld %lld",ans,n-K);return 0;
}
