题意:有一个长度为 \(n\) 的数组 \(b\),初始值全为 \(0\)。同时有一个长度为 \(m\) 的序列 \(a_i\)。依次进行操作 \(i=1,2,\dots,n\)。
- 对于操作 \(i\),可以选择 \(b\) 中任意不同的 \(a_i\) 个位置 \(j_1,j_2,\dots,j_{a_i}\),对于每个 \(p=1,2,\dots,a_i\),将 \(b_{j_p}\) 加一。
对于每一个 \(k=1,2,\dots,m\),求出,所有可能情况中,操作完所有 \(a_i\)后,\(b\) 数组中最多有多少个值为 \(k\) 的数。
\(1 \le n,m \le 2\times 10^5,1 \le a_i \le n\)。
先考虑 \(O(nm)\) 怎么做。
直接考虑对于每个 \(k\),暴力地判断每个 \(x\),是否可能出现 \(k\) 次。这两层循环是 \(O(nm)\) 的,想想 \(O(1)\) 判断。
这里判断合法有三个限制。
直观一点,把 \(a_i\) 的取值画成一个矩形区域(直方图?),看成在里面填数的过程。
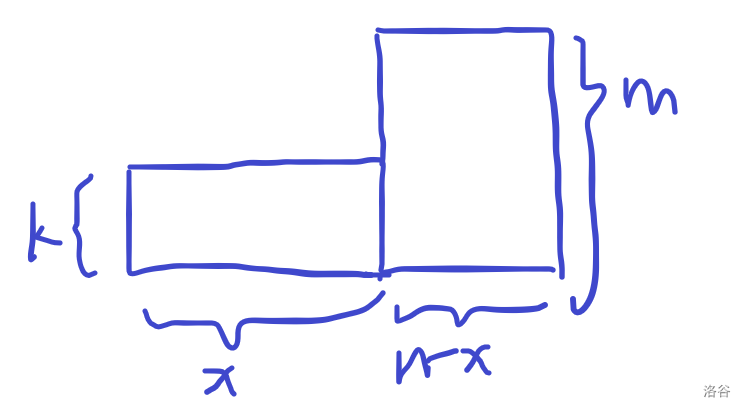
这里就可以直观地看到,左侧 \(k \times x\) 的矩形一定要填满,右侧 \(m \times (n-x)\) 的矩形可以任意填。
三个限制:
- \(a_i\) 的总和不能超过总面积。
- 能够填满 \(k \times x\) 的矩形。更具体地,\((x \cdot \sum[a_i > x]) + \sum_{a_i \le x} a_i \ge kx\)。也就是,不能将 \(a_i > x\) 的操作,一次全塞在 \(k\times x\) 的矩形里面。
- 所有大于 \(n-x\) 的 \(a_i\),【溢出】部分之和不能超过 \(kx\)。
直观感受就是,满足这三个条件,就可以任意构造出来一组解。解的构造就是,先让每个 \(a_i\) 都在右侧矩形里待着,【溢出】部分就往左边矩形里放。如果不够,再从右侧矩形里面拿来一些放进左侧矩形里。
这样预处理前缀和,就可以做到 \(O(nm)\)。
再考虑优化。
如果记 \(sum_j\) 为所有小于等于 \(j\) 的个数,\(cnt_j\) 为所有大于等于 \(j\) 的个数,那么,上面条件通过变形可以得到
\[\max(sum_n - m(n-x), sum_n - sum_{n-x} - (n-x)\cdot cnt_{n-x+1}) \le kx \le cnt_x\cdot x + sum_{x-1}
\]
然后发现对于每个 \(x\),合法的 \(k\) 是一段区间!!!并可以 \(O(1)\) 计算!!!
然后就可以不动脑子地线段树维护区间赋值。时间复杂度 \(O(n \log m)\)。
#include <bits/stdc++.h>
using namespace std;// #define filename "seq"
#define FileOperations() freopen(filename".in", "r", stdin), freopen(filename".out", "w", stdout)
//#define multi_cases 1#define inf 0x3f3f3f3f
#define Linf 0x3f3f3f3f3f3f3f3f
#define pii pair<int, int>
#define ull unsigned long long
#define all(v) v.begin(), v.end()
#define upw(i, a, b) for(int i = (a); i <= (b); ++i)
#define dnw(i, a, b) for(int i = (a); i >= (b); --i)template<class T> bool vmax(T &a, T b) { return b > a ? a = b, true : false; }
template<class T> bool vmin(T &a, T b) { return b < a ? a = b, true : false; }
template<class T> void clear(T &x) { T().swap(x); }const int N = 2e5+2;#define int long longint n, m;
int a[N];namespace SegmentTree {struct node {node *l, *r;int val;int tag;void upd(int v) { val = v, tag = v; }void down() { if(tag) l->upd(tag), r->upd(tag), tag = 0; }} pool[N << 1], *tmp = pool;node *newnode() {tmp->l = tmp->r = NULL;tmp->val = tmp->tag = 0;return tmp++;}struct Sgt {node *root;int l, r;void build(node *&p, int l, int r) {p = newnode();if(l == r) return;int mid = l + r >> 1;build(p->l, l, mid), build(p->r, mid+1, r);}void build(int l, int r) {this->l = l, this->r = r;build(root, l, r);}void update(node *p, int l, int r, int ql, int qr, int v) {if(l == ql && r == qr) return p->upd(v);int mid = l + r >> 1;p->down();if(mid >= qr) update(p->l, l, mid, ql, qr, v);else if(mid < ql) update(p->r, mid+1, r, ql, qr, v);else {update(p->l, l, mid, ql, mid, v);update(p->r, mid+1, r, mid+1, qr, v);}}void update(int ql, int qr, int v) { update(root, l, r, ql, qr, v); }void print(node *p, int l, int r) {if(l == r) return printf("%lld ", p->val), void();int mid = l + r >> 1;p->down();print(p->l, l, mid), print(p->r, mid+1, r);}void print() { print(root, l, r); }};
}SegmentTree::Sgt tr;void WaterM() {cin >> n >> m;upw(i, 1, m) scanf("%lld", &a[i]);vector<long long> cnt(n+2), sum(n+2);upw(i, 1, m) ++cnt[a[i]], sum[a[i]] += a[i];upw(i, 1, n) sum[i] += sum[i-1];dnw(i, n, 1) cnt[i] += cnt[i+1];tr.build(1, m);upw(x, 1, n) {int l = (max(sum[n] - m * (n-x), sum[n] - sum[n-x] - (n-x) * cnt[n-x+1]) + x - 1) / x;int r = (cnt[x] * x + sum[x-1]) / x;vmax(l, 1ll), vmin(r, m);if(l <= r) tr.update(l, r, x);}tr.print();puts("");
}signed main() {
#ifdef filenameFileOperations();
#endifsigned _ = 1;
#ifdef multi_casesscanf("%d", &_);
#endifwhile(_--) WaterM();return 0;
}