1. 定义
有N个集合,称为 S[1],s[2]...s[n] ,则这N个集合的并集为
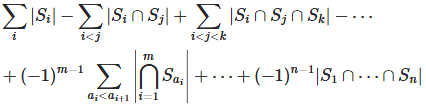
假如有N个毫不相干的约束条件,那么可以将所有满足某个约束条件的状态看作一个集合,这样用容斥原理就可以很轻松地求出所有满足至少一个约束条件的状态总数
2. 题目
洛谷P1287 盒子与球
https://www.luogu.com.cn/problem/P1287
由于盒子互不相同,可以将第i个盒子为空看作一个约束条件,这样可以求出至少有一个空盒的状态总数,再用总答案减去不合法答案就行了

点击查看代码
#include <iostream>
using namespace std;
int qpow(int a,int b){int res=1;while(b){if(b&1){res=res*a;} a=a*a;b=(b>>1);}return res;
}
int c(int a,int b){int res=1;for(int i=a;i>=a-b+1;i--){res*=i;}for(int i=b;i>=1;i--){res/=i;}return res;
}
int main(){int n,m;cin>>n>>m;int ans=0;//不合法方案 int opt=1;for(int i=1;i<=m;i++){//至少i个空盒 ans+=opt*c(m,i)*qpow(m-i,n);opt=-opt;}cout<<qpow(m,n)-ans;
}

洛谷P1450 [HAOI2008] 硬币购物
https://www.luogu.com.cn/problem/P1450
这道题可以将第i种硬币用的数量超了看作一个约束条件,提前处理出来无限背包的情况,同样是用总数减去不合法的总数
这里有一个小技巧,可以用二进制数从1到16遍历,用有几位是1来判断加还是减

点击查看代码
#include <iostream>
#define int long long
using namespace std;
const int MAX=1e5+7;
int c[5];
int f[MAX];//滚动数组,付i元的方案数
int d[5];
signed main(){for(int i=1;i<=4;i++){cin>>c[i];}f[0]=1;//初始化 for(int i=1;i<=4;i++){for(int j=c[i];j<MAX;j++){f[j]+=f[j-c[i]];//无限背包 }}int T;cin>>T;while(T--){for(int i=1;i<=4;i++){cin>>d[i];}int s;cin>>s;int ans=0;//不合法数量 for(int i=1;i<16;i++){//0001-->1111int left=s,opt=-1;for(int j=1;j<=4;j++){if((i&(1<<(j-1)))!=0){//第j项超了 left-=(d[j]+1)*c[j];opt=-opt;}}if(left>=0){ans+=opt*f[left];}}cout<<f[s]-ans<<endl;}
}

3. 总结
容斥原理的一般思路就是用总数减去所有不合法的数目
在计数题,不合法的情况可以拆分成若干个小条件,且满足小条件的总数很容易求时可以考虑容斥原理
一般会搭配 快速幂,排列组合,逆元,乘法原理 等结合出题
算是数学与信息的结合,比较抽象,考场上可能很难看出是容斥原理
更多信息请参考
https://oi-wiki.org/math/combinatorics/inclusion-exclusion-principle/
