CF1237 C2. Balanced Removals (Harder)
题目描述
这是该问题的更难版本。在本版本中,\(n \le 50\,000\)。
在三维空间中有 \(n\) 个互不相同的点,编号从 \(1\) 到 \(n\)。第 \(i\) 个点的坐标为 \((x_i, y_i, z_i)\)。点的数量 \(n\) 是偶数。
你需要通过一系列 \(\frac{n}{2}\) 次“消除”操作移除所有 \(n\) 个点。每次操作,你可以移除任意两个尚未被移除且构成“完全平衡对”的点 \(a\) 和 \(b\)。如果不存在其他尚未被移除的点 \(c\) 位于点 \(a\) 和 \(b\) 的轴对齐最小包围盒内,则点对 \(a\) 和 \(b\) 被称为“完全平衡对”。
形式化地说,若且唯若 \(\min(x_a, x_b) \le x_c \le \max(x_a, x_b)\),\(\min(y_a, y_b) \le y_c \le \max(y_a, y_b)\),且 \(\min(z_a, z_b) \le z_c \le \max(z_a, z_b)\),则点 \(c\) 位于点 \(a\) 和 \(b\) 的轴对齐最小包围盒内。注意,包围盒可能是退化的。
请找出一种方案,用 \(\frac{n}{2}\) 次操作移除所有点。
输入格式
第一行包含一个整数 \(n\)(\(2 \le n \le 50\,000\),\(n\) 为偶数),表示点的数量。
接下来的 \(n\) 行,每行包含三个整数 \(x_i, y_i, z_i\)(\(-10^8 \le x_i, y_i, z_i \le 10^8\)),表示第 \(i\) 个点的坐标。
任意两点不会重合。
输出格式
输出 \(\frac{n}{2}\) 行,每行两个整数 \(a_i, b_i\)(\(1 \le a_i, b_i \le n\)),表示第 \(i\) 次操作中被移除的两个点的编号。每个 \(1\) 到 \(n\) 之间的整数恰好出现一次。
可以证明总是存在一种移除所有点的方案。如果有多种方案,输出任意一种即可。
输入输出样例 #1
输入 #1
6
3 1 0
0 3 0
2 2 0
1 0 0
1 3 0
0 1 0
输出 #1
3 6
5 1
2 4
输入输出样例 #2
输入 #2
8
0 1 1
1 0 1
1 1 0
1 1 1
2 2 2
3 2 2
2 3 2
2 2 3
输出 #2
4 5
1 6
2 7
3 8
说明/提示
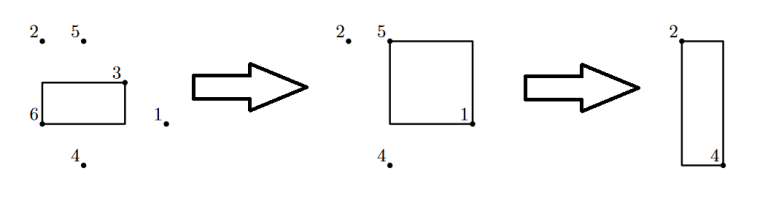
在第一个样例中,点及其对应的包围盒如下图所示(为简化起见,仅在 \(z=0\) 平面上绘制)。注意,移除的顺序很重要:例如,点 \(5\) 和 \(1\) 最初并不能构成完全平衡对,但在点 \(3\) 被移除后可以。
由 ChatGPT 4.1 翻译
solution
本来大概想到了的,但是WA了又发了会呆感觉不会写了,于是看了一眼题解才意识到本来想得没啥问题。
考虑一维的情况,肯定优先移除 \(x\) 相等的点,于是不存在 \(x\) 相等的点对了,可以直接按 \(x\) 排序后移除相邻的对。
二维呢?类似地,对于 \(x\) 相等的点,它们的 \(y\) 又构成了一维的情况,于是不会再有 \(x\) 相等的点对,于是又可以按 \(x\) 排序后移除相邻的点,因为它们之间不会有 \(x\) 在它们之间的数字了。
三维的话,\(x\) 相同的点又可以构成二维的情况。类似地处理就好了。虽然这样看起来有点麻烦,但是在代码里其实就非常简单了。
#include<bits/stdc++.h>
using namespace std;
// created: 2025-09-11 21:00:46
struct node{int x, y, z, id;
};
void solve(){int n; cin >> n;vector<node> p(n);for(int i = 0; i < n; i++){cin >> p[i].x >> p[i].y >> p[i].z;p[i].id = i + 1;}sort(p.begin(), p.end(), [](node x, node y){if(x.x == y.x) return x.y == y.y ? x.z < y.z : x.y > y.y;return x.x < y.x;});vector<array<int, 2>> ans;{vector<node> np;vector<int> vis(n);for(int i = 0; i + 1 < p.size(); i++){if(p[i].x == p[i + 1].x && p[i].y == p[i + 1].y){ans.push_back({p[i].id, p[i + 1].id});vis[i] = vis[i + 1] = 1;i++;}}for(int i = 0; i < n; i++)if(!vis[i]) np.push_back(p[i]);p = np;}{vector<node> np;vector<int> vis(p.size());for(int i = 0; i + 1 < p.size(); i++){if(p[i].x == p[i + 1].x){ans.push_back({p[i].id, p[i + 1].id});vis[i] = vis[i + 1] = 1;i++;}}for(int i = 0; i < vis.size(); i++)if(!vis[i]) np.push_back(p[i]);p = np;}for(int i = 0; i < p.size(); i += 2)ans.push_back({p[i].id, p[i + 1].id});for(auto [x, y] : ans)cout << x << " " << y << "\n";
}
int main(){ios::sync_with_stdio(false), cin.tie(nullptr), cout.tie(nullptr);// int t; cin >> t; while(t--){solve();} return 0;
}
