简单的树:
题意:
一颗树,每个节点有一个权值 \(c_i\)。
\(val_i\):\(i\) 为根的子树内所有 \(c_i\) 的最大值。
\(f(x,y)\):\(c_{x}\) 改为 \(y\) 后 \(val_i\) 之和。
每次询问给定 \((l,r,a)\) ,求 \(\sum\limits_{i=l}^{r}{f(a,i)}\)。
思路
首先一眼看出来几个性质:
- 每次修改只会影响当前节点到根路径上的 \(val_i\)。
- 当前节点到根路径上的 \(val_i\) 是递增的。
- 我们只关心子树最大值,但是如果 \(c_x\) 修改了,不得不取不严格次大值。
- 我们可以猜出当前节点到根路径的 \(val_i\) 的变化是规律的,并且 \(c_x\) 对当前节点到根路径 \(val_i\) 的影响也是连续的(一个后缀)。
- 询问满足可差分性,所以下面我们考虑 \(ans_{[1,r]}-ans_{[1,l-1]}\) 。
话说回来,我们考虑当前节点到根路径上单独一个节点 \(val_i\) 对 \(ans_{[1,r]}\) 的贡献(这里的 \(r\) 不是询问的 \(r\),原谅我这一生不羁放纵,爱自由):
性质三、四说了这么多,意思是:先刨除 \(val_x\) 影响。(因为后面要单独考虑它)这里我们直接把 \(c_x\) 作为子树最大值的节点和其他的分开处理,
对于前者,我们明显是要在非严格次大值的序列上统计,后者明显是在最大值序列(\(val_i\))上统计。
兄弟们,我来盗个图:(此图甚好,想必此图原作者一定非常厉害!我对此图稍作解释,如果大佬介意可以私信骂我并让我删掉这个图,被骂我也是快哉快哉)
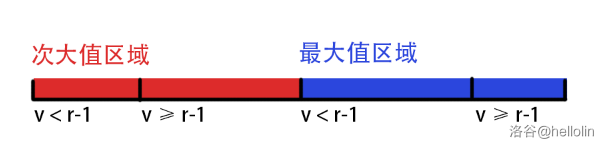
犹如上图,上图何意?
从左到右是从当前节点到根路径的刨除 \(x\) 影响的子树最大值序列。
为什么分成次大值和最大值区域?
因为我们 \(x\) 对最大值影响在这个序列上相当于一段前缀,也就是红色区域我们用次大值相当于刨除 \(x\) 影响,蓝色区域则选取最大值即可,总之,刨除 \(x\) 的影响。
上图出处:![]()
下面的 \(val_i\) 默认为刨除了 \(x\) 影响后的最大值。
当前节点到根路径上一个节点 \(val_i\) 对 \(ans_{[1,r]}\) 贡献:
- 若 \(r\le val_i\),给 \(ans_{[1,r]}\) 贡献 \(r×val_i\)。
- 若 $r>val_i $,那么相当于一个分段函数(左先平后增):
关于这种类型的东西,我们画一个柱状图就好了(因为你画分段函数真的很容易算错,尤其是重叠的边)
会给 \(ans_{[1,r]}\) 贡献:
\(val_i×val_i+[r-(val+1)+1]×(val+1+r)÷2\)
优秀的拆分:
\((r^2+val_i^2+r-val_i)÷2\)
又因为 \(r\) 在这次询问固定,\(val_i\) 随着深度减小而递增,所以 \(r\le val_i\) 和 \(r>val_i\) 的区域在序列上是一个前缀一个后缀。
重剖 + 线段树就可以很快地到根路径查了,当然你会发现这题只有向上倍增,所以可以直接写倍增,写倍增也是快哉快哉,写重剖也是应在江湖悠悠。
小言如何维护:
在线段树上维护 \(val_i^2\)、\(val_i\)、\(次val_i^2\)、\(次val_i\),然后 \(r\) 有关的东西都提出来处理。(原谅我的中文变量名,况且现在 c++20 可以用中文变量名了)。
算法流程(综上):
把给你的树重链剖分,并在线段树上维护最大值平方和,最大值和,次大值平方和、次大值。
给你一组询问 \((l,r,a)\),答案为 \((ans_{[1,r]}-ans_{[1,l-1]})\)。
对于 \(ans_{[1,k]}\),我们把先找到非严格次大值小于 \(val_x\) 且深度最小的节点 \(p\),对于 \(a\) 到 \(p\) 的路径我们用次大值维护的线段树数组计算,对于 \(fa[p]\) 到根节点的路径我们用最大值维护的线段树数组计算。注意下面的 \(val_i\) 一个路径指次大值一个路径指最大值,在这两条路径上,我们都倍增出深度最小的 \(val_i< r\) 的位置 \(q\),那么对于当前路径从这个路径起点 到 \(q\) 查 $r>val_i $ 时的贡献,对于 \(fa[q]\) 到这个路径终点查另一个丑式子(线段树查询)。
最后别忘了是整棵树的 \(val_i\) 之和(下面的 \(val_i\) 都是子树最大值),所以要把除了 \(a\) 到根路径的 \(val_i\) 加上并乘 \((r-l+1)\),这里可以容斥:用全树的 \(val_i\) 减去 \(a\) 到根路径上的 \(val_i\),然后再乘 \((r-l+1)\),再加上就行了。
至于倍增做法,非常简单,把上面的线段树都改成倍增数组,跳链都改成倍增就可以了,不得不说倍增是真简洁,至于为什么全篇尽是树剖……老师讲的树剖 QAQ,我这种蒟蒻也是倍增倍增~
代码
代码也是呼之欲出~
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int QAQ=5e5+7;
const ll mo=998244353;
int n,q,op,s[QAQ],ma[QAQ][21],cima[QAQ][21],ma2[QAQ][21],cima2[QAQ][21],f[QAQ][21],shen[QAQ],all,ni;
vector<int> dian[QAQ];
inline void dfs1(int x,int fa)
{shen[x]=shen[fa]+1,f[x][0]=fa,ma[x][0]=s[x],cima[x][0]=0;for(int i=1;i<=20;i++) f[x][i]=f[f[x][i-1]][i-1];for(int i=0;i<(int)dian[x].size();i++){int v=dian[x][i];if(v==fa) continue;dfs1(v,x);if(ma[v][0]>ma[x][0]) cima[x][0]=max(ma[x][0],cima[v][0]),ma[x][0]=ma[v][0];else cima[x][0]=max(cima[x][0],ma[v][0]);}ma2[x][0]=1ll*ma[x][0]*ma[x][0]%mo,cima2[x][0]=1ll*cima[x][0]*cima[x][0]%mo;all=(all+ma[x][0])%mo;
}
inline void dfs2(int x,int fa)
{for(int i=1;i<=20;i++)ma[x][i]=(ma[x][i-1]+ma[f[x][i-1]][i-1])%mo,cima[x][i]=(cima[x][i-1]+cima[f[x][i-1]][i-1])%mo,ma2[x][i]=(ma2[x][i-1]+ma2[f[x][i-1]][i-1])%mo,cima2[x][i]=(cima2[x][i-1]+cima2[f[x][i-1]][i-1])%mo;for(int i=0;i<(int)dian[x].size();i++){int v=dian[x][i];if(v==fa) continue;dfs2(v,x);}
}
inline int ksm(int shi,int k)
{ll da=1,x=shi;for(;k;k=k/2,x=x*x%mo) if(k&1) da=da*x%mo;return da;
}
inline int ans(int x,int r)
{if(!r) return 0;int p=x,o1=x,o2,o3,o4;for(int i=20;i>=0;i--) if(f[p][i]&&shen[f[p][i]]>=shen[1]&&cima[f[p][i]][0]<s[x]) p=f[p][i];o2=p,o3=f[p][0],o4=1;if(cima[p][0]>=s[x]) o2=-114514,o3=x;// 下面是次大值区域 int da=0,nw;int da2=0,len=0;if(o2!=-114514){p=o1;for(int i=20;i>=0;i--)if(f[p][i]&&shen[f[p][i]]>=shen[o2]&&cima[f[p][i]][0]<r) p=f[p][i];if(cima[p][0]<r) nw=f[p][0];else nw=p;for(int i=20;i>=0;i--) if(f[nw][i]&&shen[f[nw][i]]>=shen[o2]) da=(da+1ll*r*cima[nw][i]%mo)%mo,nw=f[nw][i];if(nw==o2) da=(da+1ll*r*cima[nw][0]%mo)%mo,nw=f[nw][0];if(cima[p][0]<r){nw=o1;for(int i=20;i>=0;i--) if(f[nw][i]&&shen[f[nw][i]]>=shen[p]) da2=(da2+cima2[nw][i]-cima[nw][i]+mo)%mo,len+=(1<<i),nw=f[nw][i];if(nw==p) da2=(da2+cima2[nw][0]-cima[nw][0]+mo)%mo,nw=f[nw][0],len++;da2=((da2+1ll*len*r*r%mo+1ll*len*r%mo)*ni)%mo;da=(da+da2)%mo;}}//下面是最大值区域 if(o3){p=o3;for(int i=20;i>=0;i--)if(f[p][i]&&shen[f[p][i]]>=shen[o4]&&ma[f[p][i]][0]<r) p=f[p][i];if(ma[p][0]<r) nw=f[p][0];else nw=p;for(int i=20;i>=0;i--) if(f[nw][i]&&shen[f[nw][i]]>=shen[o4]) da=(da+1ll*r*ma[nw][i]%mo)%mo,nw=f[nw][i];if(nw==o4) da=(da+1ll*r*ma[nw][0]%mo)%mo,nw=f[nw][0];da2=0,len=0;if(ma[p][0]<r){nw=o3;for(int i=20;i>=0;i--) if(f[nw][i]&&shen[f[nw][i]]>=shen[p]) da2=(da2+ma2[nw][i]-ma[nw][i]+mo)%mo,len+=(1<<i),nw=f[nw][i];if(nw==p) da2=(da2+ma2[nw][0]-ma[nw][0]+mo)%mo,nw=f[nw][0],len++;da2=((da2+1ll*len*r*r%mo+1ll*len*r%mo)*ni)%mo;da=(da+da2)%mo;}}//下面是统计其余部分。 da=(da+1ll*all*r%mo)%mo;nw=o1;for(int i=20;i>=0;i--)if(f[nw][i]&&shen[f[nw][i]]+1>=shen[1]) da=((da-1ll*r*ma[nw][i]%mo)%mo+mo)%mo,nw=f[nw][i];if(nw==1) da=((da-1ll*r*ma[nw][0]%mo)%mo+mo)%mo,nw=0;return da;
}
inline int read()
{int x=0;char c=getchar();while(c<'0'||c>'9') c=getchar();while(c>='0'&&c<='9') x=(x<<3)+(x<<1)+(c^48),c=getchar();return x;
}
signed main()
{n=read(),q=read(),op=read();for(int i=1;i<=n;i++) s[i]=read();for(int i=1,u,v;i<n;i++) u=read(),v=read(),dian[u].push_back(v),dian[v].push_back(u);dfs1(1,0),dfs2(1,0),ni=ksm(2,mo-2);for(int i=1,shang=0,l,r,a;i<=q;i++){l=read(),r=read(),a=read(),l=((l+op*shang)%n)+1,r=((r+op*shang)%n)+1,a=((a+op*shang)%n)+1;if(l>r) swap(l,r);printf("%d\n",(shang=(((ans(a,r)-ans(a,l-1))%mo+mo)%mo)));}return 0;
}
这个代码写得过于傻,导致被卡了,可以循环展开一下再加上评测机波动就可以过,但是为了美感(实际上也没有),所以我在这里放的是正解代码,我已经申请增大时限了。
