前言
彩笔运维勇闯机器学习,今天我们来讨论一下梯度下降法
梯度
首先要搞明白什么是梯度,那就要先从导数说起
导数
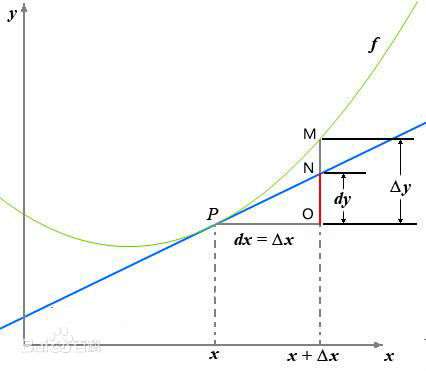
函数\(y=f(x)\)的自变量\(x\)在一点\(x_0\)上产生一个增量\(\Delta x\)时,函数输出值的增量\(\Delta y=f(x_0 + \Delta x)-f(x_0)\)与自变量增量\(\Delta x\)的比值在\(\Delta x\)趋于0时的极限\(a\)如果存在,\(a\)即为在\(x_0\)处的导数
\[f'(x) = \frac{\partial y}{\partial x} = \lim_{\Delta x \to 0} \frac{f(x + \Delta x) - f(x)}{\Delta x} = a
\]
![gradient_1]()
(该图来自于百度百科)
偏导数
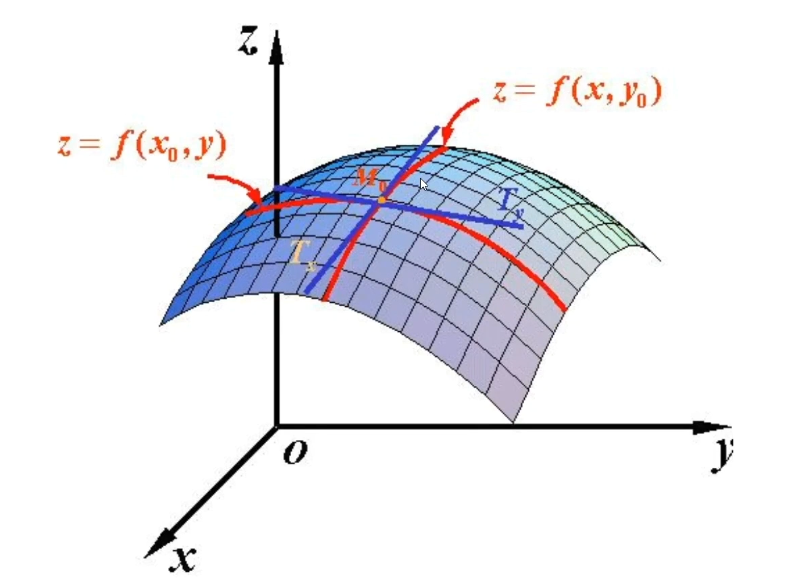
偏导数与导数的本质是一样的,只不过偏导数解决的是多变量的问题
\[\frac{\partial f}{\partial x_i} = \lim_{\Delta x_i \to 0} \frac{f(x_1, \dots, x_i + \Delta x_i, \dots, x_n) - f(x_1, \dots, x_i, \dots, x_n)}{\Delta x_i}
\]
比如二元函数\(f(x,y)\)
对\(x\)求偏导:
\[\frac{\partial f}{\partial x} = \lim_{\Delta x \to 0} \frac{f(x + \Delta x, y) - f(x, y)}{\Delta x}
\]
对\(y\)求偏导:
\[\frac{\partial f}{\partial y} = \lim_{\Delta y \to 0} \frac{f(x, y + \Delta y) - f(x, y)}{\Delta y}
\]
![gradient_2]()
(该图来自于百度百科)
超过二元的就画不出来图来了
方向导数
导数与偏导数都是自变量相对于某一轴方向(比如x相对于x轴,y相对于y轴)讨论变化率,而如果自变量可以其定义域内自由选择方向讨论变化率
一个多元函数\(f\)和一个方向向量\(u\),方向导数\(D_uf\)表示函数\(f\)在\(u\)方向的变化率
\[D_{\mathbf{u}}f(a) = \lim_{h \to 0} \frac{f(a + hu) - f(a)}{h}
\]
用二元函数举例:
\[D_{\mathbf{u}}f(x_0, y_0) = \lim_{h \to 0} \frac{f(x_0 + h u_1, y_0 + h u_2) - f(x_0, y_0)}{h}
\]
- \(u_1 u_2\)表示方向\(u = (u1, u2)\)
- h表示沿着\(u\)方向的位移
梯度
梯度是多元函数在某一点处所有偏导数构成的向量,表示函数在该点处变化最快的方向及其变化率,对于\(f(x_1,x_2,...,x_n)\),其梯度记为\(\nabla f\)
\[\nabla f = \left(\frac{\partial f}{\partial x_1}, \frac{\partial f}{\partial x_2}, \dots, \frac{\partial f}{\partial x_n}\right)
\]
- 方向:梯度指向函数在该点增长最快的方向
- 大小:梯度的模表示函数在该方向上的最大变化率
方向导数:梯度与单位方向向量u的点积
\[D_uf=\nabla f⋅u
\]
当\(u\)与\(\nabla f\)同方向时,方向导数最大
当\(u\)与\(\nabla f\)反方向时,方向导数最小
小结
梯度与方向导数:梯度是方向导数中变化率最大的那一个:梯度的方向是方向导数取最大值的方向,而梯度的模长(大小)等于该最大方向导数的值
方向导数与偏导数:偏导数是方向导数的特例,即\(u=(0,1)\),简而言之,方向导数在坐标轴上移动,就是偏导数
了解了梯度的诞生以及概念之后,终于可以来讨论一下本文的主题:梯度下降法
梯度下降法
在回归任务中,用于评估模型的重要指标是损失函数MSE,提高模型的泛化能力就是设法降低MSE
上述关于梯度的描述,梯度就是函数变化率最快的方向,那梯度下降法就是不断沿着付梯度方向寻找MSE的最小值。不同于最小二乘法只能用于线性模型,梯度下降法适用于大部分模型,包括线性回归、逻辑回归等等
核心思想
- 函数的梯度指向函数值增长最快的方向,负梯度方向则是函数值下降最快的方向
- 通过不断沿负梯度方向调整参数,逐步逼近函数的最小值点
步骤
- 初始化,随机选择初始参数或者全部设置为0
- 迭代更新,每迭代一次都会更新参数的值:$$\theta_{t+1}=\theta_t - \eta ⋅ \nabla f(\theta_t)$$
- \(\theta_t\):第\(t\)次迭代的参数值
- \(\eta\):每次更新的幅度,也叫学习率
- \(\nabla J(\theta_t)\):目标函数\(f\)在\(\theta_t\)的梯度
- 终止迭代的条件:
- 梯度很小:梯度的模长很小,一般小于\(10^{-6}\)
- 损失函数变化很小:一般小于\(10^{-6}\)
- 到达最大迭代次数
计算过程
我们用本系列的第一节:一元线性回归中的数据,用梯度下降法详细演示一次
data = {'result': [0.63, 0.72, 0.72, 0.63, 0.57, 0.52, 0.48, 0.47],'feature1': [22.48, 19.50, 18.02, 16.97, 15.78, 15.11, 14.02, 13.24]
}
目标是找到一组参数,使得损失函数MSE最小:
\[\text{MSE} = \frac{1}{n} \sum_{i=1}^{n} (y_i - \hat {y}_i)^2
\]
带入\(y=\beta_0 + \beta_1 x\)
\[f(\beta_0 , \beta_1) = \frac{1}{n} \sum_{i=1}^{n} (\beta_0 + \beta_1 x_i - \hat {y}_i)^2
\]
首先计算梯度,分别对\(\beta_0\)、\(\beta_1\)求偏导
先对\(\beta_0\)求偏导:
\[\frac{\partial f}{\partial β_0} = \frac{1}{n} \sum_{i=1}^{n} 2(β_0 + β_1x_i - \hat {y}_i)⋅(β_0 + β_1x_i - \hat {y}_i)' = \frac{2}{n} \sum_{i=1}^{n} (β_0 + β_1x_i - \hat {y}_i)
\]
在对\(\beta_1\)求偏导:
\[\frac{\partial f}{\partial β_1} = \frac{1}{n} \sum_{i=1}^{n} 2(β_0 + β_1x_i - \hat {y}_i)⋅(β_0 + β_1x_i - \hat {y}_i)' = \frac{2}{n} \sum_{i=1}^{n} (β_0 + β_1x_i - \hat {y}_i)⋅x_i
\]
至此得出梯度:
\[\nabla f = (\frac{2}{n} \sum_{i=1}^{n} (β_0 + β_1x_i - \hat {y}_i), \frac{2}{n} \sum_{i=1}^{n} (β_0 + β_1x_i - \hat {y}_i)⋅x_i)
\]
设置参数,学习率\(\eta=0.001\),迭代次数100次,开始迭代:
1)第一轮迭代,先初始化\(\beta_0\) \(\beta_1\)为0
计算损失函数:
\[\begin{aligned}
MSE &= f(\beta_0 , \beta_1) = \frac{1}{n} \sum_{i=1}^{n} (\beta_0 + \beta_1 x_i - \hat {y}_i)^2 \\&= \frac{1}{8}[(0-0.63)^2+(0-0.72)^2+...+(0-0.47)^2] = 0.35965
\end{aligned}
\]
计算梯度:
\[\begin{aligned}
\frac{\partial f}{\partial β_0} &= \frac{2}{n} \sum_{i=1}^{n} (β_0 + β_1x_i - \hat {y}_i) \\&= \frac{1}{4}[(0-0.63)+(0-0.72)+...+(0-0.47)] = -1.185
\end{aligned}
\]
\[\begin{aligned}
\frac{\partial f}{\partial β_1} &= \frac{2}{n} \sum_{i=1}^{n} (β_0 + β_1x_i - \hat {y}_i)⋅x_i \\&= \frac{1}{4}[(0-0.63)·22.48+(0-0.72)·19.50+...+(0-0.47)·13.24] = -20.418025
\end{aligned}
\]
\[\nabla f = (-1.185, -20.418025)
\]
损失函数与梯度均小于\(10^{-6}\),继续迭代第二轮
2)第二轮迭代,先初始化\(\beta_0\) \(\beta_1\)
\[\beta_0 ← \beta_0 - \eta · \frac{\partial f}{\partial β_0} = 0 - 0.001·(-1.185) = 0.001185
\]
\[\beta_1 ← \beta_1 - \eta · \frac{\partial f}{\partial β_1} = 0 - 0.001·(-20.418025) = 0.020418025
\]
计算损失函数:
\[MSE = f(\beta_0 , \beta_1) = \frac{1}{n} \sum_{i=1}^{n} (\beta_0 + \beta_1 x_i - \hat {y}_i)^2 = 0.064501 \\
\]
计算梯度:
\[\frac{\partial f}{\partial β_0} = \frac{2}{n} \sum_{i=1}^{n} (β_0 + β_1x_i - \hat {y}_i) = -0.492909
\]
\[\frac{\partial f}{\partial β_1} = \frac{2}{n} \sum_{i=1}^{n} (β_0 + β_1x_i - \hat {y}_i)⋅x_i = -8.395268
\]
\[\nabla f = (-0.492909, -8.395268)
\]
损失函数与梯度均小于\(10^{-6}\),继续迭代第三轮...
就这样不断迭代下去,直至满足停止的条件,停止之后,该轮次的\(β_0\) \(β_1\)就是最佳参数
联系我
![]()
至此,本文结束
在下才疏学浅,有撒汤漏水的,请各位不吝赐教...