2.1 信息存储
大多数计算机使用8位的块,或者字节,作为最小的可寻址的内存单位。
机器级程序将内存视为一个非常大的字节数组,称为虚拟内存。
内存的每个字节用唯一的数字标识,称为它的地址。
所有可能地址的集合称为虚拟地址空间。
例如:C语言中一个指针的值都是某个存储块的第一个字节的虚拟地址。
十六进制表示法
十六进制,简写为:\(hex\)。
以\(0x\)或\(0X\)开头的视为十六进制的值。
以\(0b\)开头的视为二进制的值。
如果位总数不是4的倍数,那么最前端可以用0补足。
对于某个\(2\)的整数幂,我们可以写成\(0x800\)等的形式,表示\(2^{11}\)。
字数据大小
每台计算机都有一个字长,表示指针数据的标称大小。
字长决定的最重要的系统参数是虚拟地址空间的最大大小,如果字长为\(w,\)则最多访问\(0 \sim 2^w-1\)的虚拟地址范围,即\(2^w\)个字节。
基本C数据类型的典型大小:在32位和64位机器上,long/unsigned long分别表示4个字节和8个字节,而char* 分别表示4个字节和8个字节,注意它与char的区分。
注意:char也能用来存储具体数值,同时,它没有无符号生命(尽管大多数语言视为有符号数,但是C不保证)。
注意:unsigned long/long unsigned 无论加上int都还是原样。
注意:float,double分别占用4字节和8字节,这点在后面会讲到。
基本C数据类型的典型大小

寻址与字节顺序
多字节对象被存储为连续的字节序列,每个对象有唯一的索引,即地址。对象的地址为使用字节中最小的地址。标号较小的地址称为称为低地址,标号较大的地址称为高地址。在多字节数据的存储中,地址的排列方式被称为字节序。
小端法:最低有效字节在前面(低地址),即从高地址向低地址排。
大端法:最高有效字节在前面(低地址),即从低地址向高地址排。
另外,还有双端法
反汇编器:确定可执行程序文件所表示的指令序列的工具
C语言中,有强制类型转换,这个后面会讲到
sizeof:确定对象使用的字节数
表示字符串&表示代码
C中字符串是一个以Null结尾的字符数组
在使用Ascil码的任何系统上都得到相应的结果,与字节顺序与字大小规则无关,比二进制码平台独立性更强。
从机器的角度来看,程序仅仅是字节序列。
布尔代数简介
与、或、非、异或,进而拓展到位向量
例子:用位向量对集合编码
C语言中的位级运算
掩码,用0xFF来生成由x的最低有效字节组成的值,即x&0xFF.
广义上通常用于取出某个数中的某些位,我们将在lab中见到这一点。
C语言中的逻辑运算
逻辑运算很容易和位级运算混淆,即逻辑与(&&),逻辑或(||),与逻辑非(!)。
- 所有逻辑运算的值只能是0或1,其将非零数视为真,将零视为假,\(!\)和\(!!\)常用于将非零数转化为\(1,\)这点在lab中有所体现。
- 对于&&和||,如果第一个表达式就可以确定结果,那么不会求后续表达式的值。也被称为短路行为。
C语言中的移位运算
- 左移就是在右边补0,右移分为算术右移和逻辑右移,逻辑右移就是在左边补零,算术 右移就是在左边补上最高有效位的值
- 对于非负数,算术右移和逻辑右移的效果是一样的,因此对于无符号数,右移都是逻辑右移。而在\(C\)中,有符号整数是算术右移。
注意:加法与减法的优先级比移位运算高,因此我们需要加上括号。
注意:应该保持位移量小于带位移值的位数。
2.2 整数表示
下图是我们常用的数学公式与符号:
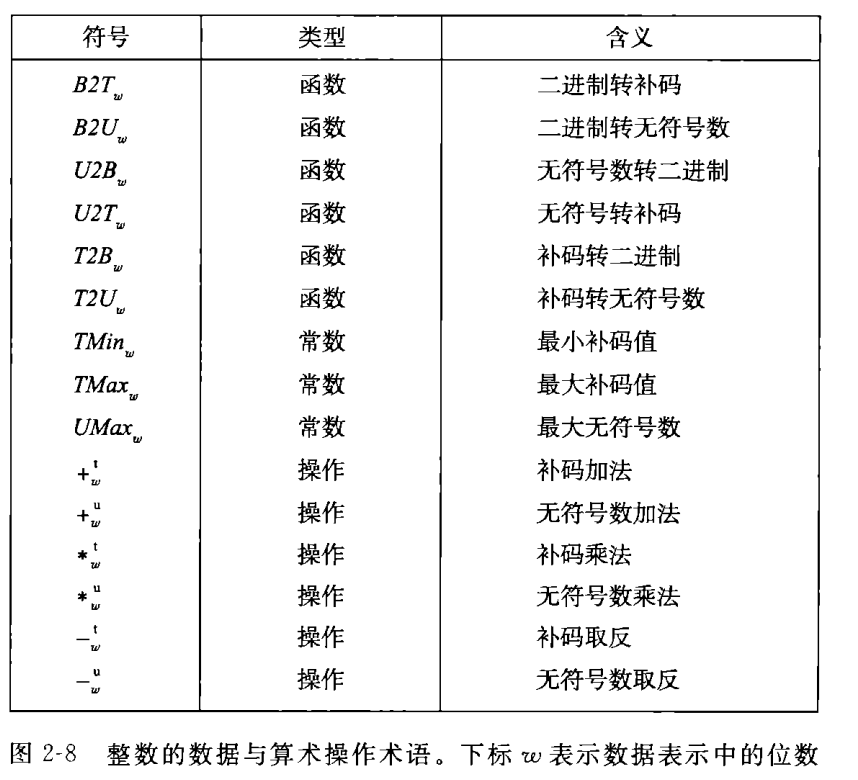
整型数据类型
注意:int32_t,uint32_t,int64_t,uint64_t都是固定取值。
同时,正数和负数的取值范围不是对称的,并且\(C\)语言标准定义了每种数据类型必须能够表示的最小数据范围,而这比实际的范围小得多,固定大小的数据类型保证数值范围与典型数值一致。
无符号数的编码
无符号数编码是唯一的。
补码编码
最高位取\(-2^{w-1}\)。
补码编码是唯一的。并且\(|TMIN|=|TMAX|+1.\)
有符号数的其他两种表示方法:
- 反码:最高有效位的权是\(-(2^{w-1}-1),\)其余与补码相同。
- 原码:最高有效位是符号位,表示\((-1)^x\)。浮点数中使用原码编码。
有符号数和无符号数之间的转换
注意:强制类型转换的结果保持位值不变,只是改变了解释这些位的方式。
- 补码转化为无符号数:负数加\(2^w,\)非负数不变。
- 无符号数转化为补码:高于\(TMax\)减去\(2^w,\)反之不变。
C语言中的有符号数和无符号数
\(C\)语言自动将常量视为有符号的,因此在创建这样的常量时,需要在后面加\(U\)使其变为无符号常量。有符号数和无符号数之间可以发生转换:
- 隐式转换:当一种类型的表达式被赋值给另一种类型的表达式
- 显式转换:强制类型转换
- 特殊的隐式转换:当一个运算中,一个运算数是有符号的而另一个是无符号的,那么会将有符号参数转换为无符号参数
拓展一个数字的位表示
拓展一个数字的位表示,就是把它从较小的数据类型转换到较大的类型:
- 无符号数的零拓展:直接在左边加0
- 补码数的符号拓展:在左边重复最高有效位
例:将short转换为unsigned时,我们先改变大小,然后发生从有符号数到无符号数的转换。
截断数字
我们有时候需要减少表示一个数字的位数:
- 截断无符号数:截断为\(k\)位,相当于直接\(\mathrm{mod} \ k\).
- 截断补码数值:先转换为无符号数,然后再截断。
关于有符号数和无符号数的建议
下面引入一个例子:
计算(unsigned)0-1:
- 先将1转化为unsigned类型
- 0-1 \(\equiv 2^{32}-1 (\mathrm{mod} \ 2^{32}) = 0xFFFFFFFF\)
2.3 整数运算
加法
- 无符号加法:若\(x+y \geq 2^w,\)则发生溢出,需要减去\(2^w.\)
- 检验无符号数加法是否溢出:若溢出,则\(x+y < x \vee x+y < y.\)
- 补码加法:若\(x+y \geq 2^{w-1},\)则发生正溢出,需要减去\(2^{w-1},\)若\(x+y<-2^{w-1},\)则发生负溢出,需要加上\(2^{w-1}.\)
- 检验补码加法是否溢出:若\(x>0,y>0,x+y \le 0,\)则发生正溢出;若\(x<0,y<0,x+y \ge 0,\)则发生负溢出。
注意:补码加法和无符号数加法都是阿贝尔群
补码的非
- 若x!=INT_MIN,x的补码是-x.
- 若x==INT_MIN,x的补码是INT_MIN.
下面我们介绍如何求补码的非:
- 对二进制取反加1
- 对最右边的1左边的所有部分取反(不包含这个1)
乘法
- 无符号乘法:\(x * y=(x \cdot y) \mathrm{mod} \ 2^w.\)
- 补码乘法:\(x * y = U2T_w((x \cdot y)\mathrm{mod} \ 2^w).\)
- 无符号乘法和补码乘法在位上是等价的.
- 乘以常数:乘以\(2^w\),即左移w位,然后相加或相减,视具体情况而定。
注意:程序可能在毫无察觉的情况下产生乘法溢出。
除法
在介绍除法之前,我们有以下前提,整数除法总是舍入到零.
- 无符号除法:除以\(2^w,\)即逻辑右移w位。
- 补码除法:当\(x>0,\)此时逻辑右移与算术右移相同,即x>>w;当\(x<0,\)此时向上舍入,得到(x+(1<<w)-1)>>w.
注意:当除数的幂次比较小时,我们有比较简单的做法,具体见lab.
2.4 浮点数
无论是整数还是小数,在计算机中都是由二进制表示的,与十进制相同,我们可以定义\(0.x_1x_2\ldots x_k=x_1*2^{-1}+\ldots +x_k*2^{-k},\)进而采用IEEE浮点格式来近似表示浮点数。
IEEE浮点格式
在IEEE浮点格式中,单精度浮点数(float)和双精度浮点数(double).它们都分为符号位(S)、指数位(Exp)和尾数位(Frac):
- 符号位:表示这个数是非负数还是负数
- 指数位:表示这个数的指数,但是与最终结果的指数不同
- 尾数位:表示这个数小数部分
注意:在单精度浮点数中,有1位符号位,8位指数位,22位尾数位;在双精度浮点数中,有1位符号位,11位指数位,52位尾数位。
在IEEE浮点格式中,有三种情况:
规格化的值(最普遍的情况)
- 若Exp的位模式不全为0或1,即为规格化的值。此时,我们引入偏置值(
bias),其等于\(2^{w-1}-1,w\)为指数位的位数。实际指数\(e=Exp-bias\)。 - 在单精度中,\(Exp \in [1,254],bias=127\)即\(e \in [-126,127].\)
- 尾数位则表示\(1.x_1x_2\ldots x_k,\)实际需要将其补零右对齐.
- 计算规格化值,则为\((-1)^s \cdot 2^{e} \cdot frac.\)
非规格化值
- 若Exp的位模式全为0,即为非规格化的值。此时我们定义\(E=1-bias.\)
- 在单精度中,此时\(E=-126.\)
- 我们定义尾数位为\(0.x_1x_2\ldots x_k,\)实际需要将其补零对齐.
- 若尾数部分也为0,则根据符号位将其分为正零和负零,便于极限计算与求正负无穷。
特殊值
- 若Exp的位模式全为1时,即为特殊值。
- 当尾数位全为0时,根据符号位将其分为正负无穷,可以表示溢出的结果。
- 当尾数位非0时,结果为Not a Number(
NaN),常用于表示未初始化的数据。
数字示例
IEEE的浮点数定义:
- 让我们能在\(\frac{7}{512}\)和\(\frac{8}{512}\)中得到平滑转变,即把E定义为1-Bias。
- 同时,非规格数的定义,使得越靠近原点数的分布更加稠密。
- 可以尝试训练一下计算最小正数,最大非规格化数,最小规格化数,最大规格化数等,对理解会有帮助
浮点数的比较
1.浮点数的比较可以参考无符号整型的规则。
2.注意特殊情况:
- \(-0=+0\)
- NaN与任何数比较都返回False,NaN!=NaN返回True.
浮点数运算与舍入
浮点数定义了四种不同的舍入方式,分别是:
- 向零舍入
- 向下舍入
- 向上舍入
- 向偶数舍入,也被称为向最接近的值舍入,也是IEEE的默认方法。即若一个值位于两个要表示的值中间,则将它们舍入到最接近的偶数;反之则舍入到最接近的可表示值。这一点是初学者可能所不理解的。
浮点运算的基本思路
1.加法时,先将两个数的指数位对齐。
2.执行运算后,进行规格化。
3.若结果超出范围,则处理溢出。
4.按照规则进行舍入。
加法规则
1.对齐尾数,将指数较小的一方尾数右移。
2.按照符号位进行加减运算。
3.规范化、舍入,并处理特殊情况。
乘法规则
1.符号位相加并模2
2.实际指数e相加,若溢出则结果为无穷。
3.小数部分相乘,并按照指定精度舍入。
C语言中的浮点型规则
1.int \(\rightarrow\) float:不会溢出,可能被舍入。
2.int/float \(\rightarrow\) double,能够保留确切数值。
3.double \(\rightarrow\) float,可能被舍入,也可能溢出为\(+\infty\)或\(-\infty\)。
4.float/double \(\rightarrow\) int,向零舍入。
