复杂度分析
同一问题可能存在多种算法,而在实际运用中,往往要根据情况选择某方面最优或者最合适的算法。为此,需要对有关算法的性能进行分析和比较。目前一般用算法执行过程所耗用的计算资源总量作为算法性能的衡量指标。时间资源和空间资源是最主要的两种计算资源。已知输入数据的规模,可以用时间复杂度来大致地度量算法所耗用的时间资源,而用空间复杂度来大致地度量算法所耗用的空间资源。
对算法的时间复杂度和空间复杂度进行分析,统称为算法的复杂度分析。在未加任何限定或特殊说明的情况下,算法的时间复杂度和空间复杂度指的都是最坏情况下的复杂度。
在算法的复杂度分析中,常用大 O 记号表示算法的时间或空间复杂度在渐进意义下的量级,例如 \(O(n), O(n \log n), O(n^c), O(2^n)\) 等。这里的 n 是输入数据规模以比特为单位的计数。在输入数据的各元素采用定长表示例如字节时,\(n\) 也可以采用输入数据规模在该定长单位下的计数,例如字节数等,这不会改变算法的时间或空间复杂度在渐进意义下的量级。
大 O 记号是德国数学家 Paul Bachmann 和 Edmund Landau 在 19 世纪末左右引入的,其作用是刻画给定函数 \(f\) 在渐进意义下的量级。对于函数 f 和 g,如果有某个常数 \(c\),使得对所有足够大的正整数 \(n\) 都有 \(|f(n)| \le c|g(n)|\),则可以写做 \(f(n) = O(g(n))\)。在这里,对于给定的函数 \(g\),\(O(g(n))\) 是所有满足上述关系的函数 \(f\) 组成的集合。在 \(O(g(n))\) 出现在等号右侧时,等号所表达的是与集合相关的关系,而非数值意义上的相等关系或者其他数学等价关系。此外,该关系往往不是对称的。
例如,\(f(n)=O(g(n))\) 的严格含义是 \(f(n) \in O(g(n))\),而 \(O(f(n))=O(g(n))\) 的严格含义则是 \(O(f(n)) \subseteq O(g(n))\)。在此意义下,\(O(g(n))=f(n)\) 的写法是完全错误的。等号在这里的含义比较多样而且容易引起混淆,但因历史习惯原因而一直沿用至今。
如果某两个算法具有相同量级的时间或空间复杂度,其耗用的计算时间或存储空间仍可能具有一定的差异。在对具体的算法分析复杂度时,为了分析和计算的简便,往往会在不影响量级的前提下,忽略一些不重要的细节。
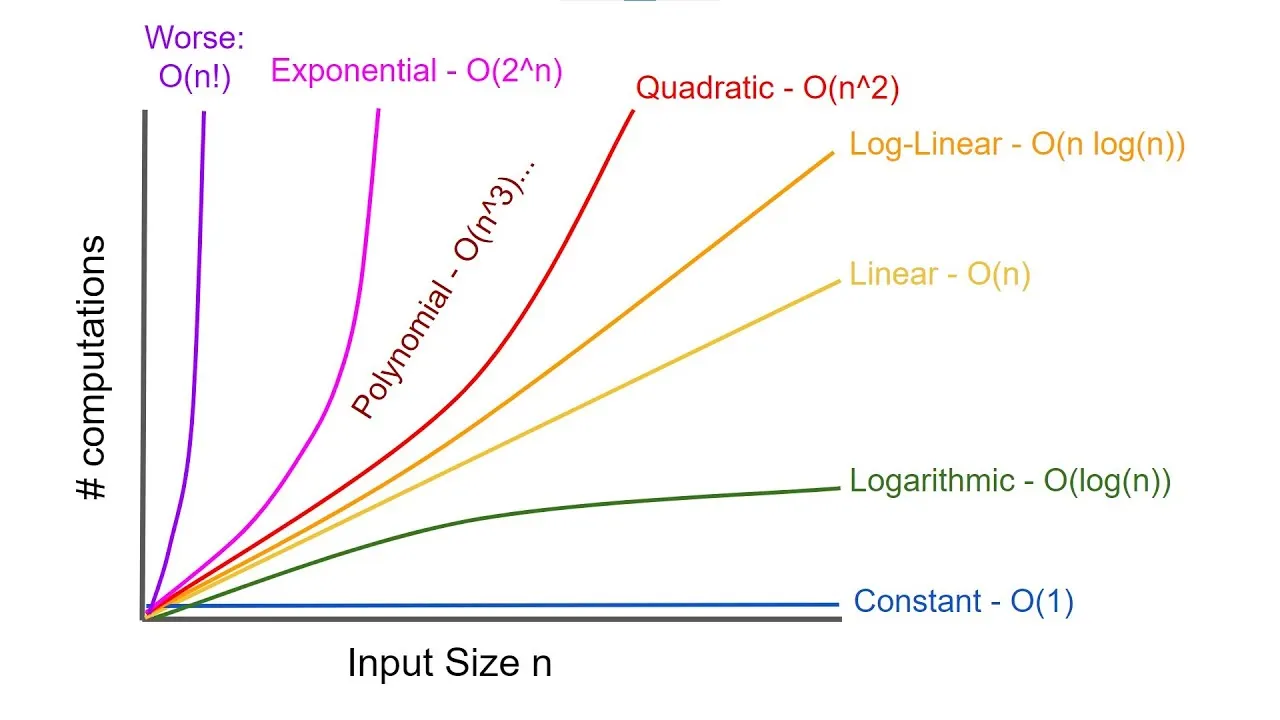
在大 O 记号的意义下,算法的复杂度的量级可以有多种刻画方式,例如某个算法的时间复杂度是 \(O(n)\),那么也是 \(O(n^2)\)。为了算法复杂度分析的准确性,往往选择最低的量级来刻画分析的结果。常用量级在渐进意义下的排序为:\(1 \prec \log \log n \prec n^{\epsilon} \prec n \prec n \log n \prec n^c \prec n^{\log n} \prec c^n \prec n! \prec n^n \prec c^{c^n}\)。
这里的 \(\epsilon\) 和 \(c\) 分别是某个满足 \(0 \lt \epsilon \lt 1 \lt c\) 的常数。符号 \(\prec\) 用来比较两个函数的量级,其含义是:如果有 \(\lim\limits_{n \rightarrow \infty} \dfrac{f(n)}{g(n)} = 0\),则写做 \(f(n) \prec g(n)\)。
时间复杂度分析
算法的时间复杂度,指的是算法在整个执行过程中所耗用的计算时间的总量,一般表示成关于输入数据规模的某个函数。由于对算法耗用时间的精确计数往往难以实现,而且也没有特别重要的意义,因此在算法的时间复杂度分析中,常用大 O 记号来给出算法时间复杂度在渐进意义下的量级。
算法的时间复杂度分析,一般通过对算法所执行的基本操作进行计数来实现。这里的基本操作,指的是耗用时间为某个固定量的操作,包括赋值、基本的数学运算和逻辑运算等。因此,算法所耗用的时间总量和算法所执行的基本操作的数量之间具有接近于线性的相关关系。一般来说,在同等规模的不同输入数据上,算法的执行时间不同。算法的时间复杂度,一般特指算法在最坏情况下所耗用的时间。
按照时间复杂度的量级,可以对算法进行分类。例如时间复杂度为 \(O(1)\) 的算法,一般被称为常数时间算法;时间复杂度为 \(O(\log n)\) 的算法,一般被称为对数时间算法;时间复杂度为 \(O(n)\) 的算法,一般被称为线性时间算法;时间复杂度为 \(O(n^c)\) 的算法(这里有 \(1 \lt c\)),一般被称为多项式时间算法;时间复杂度为 \(O(2^n)\) 的算法,属于指数时间算法。以大 O 记号所刻画的算法时间复杂度,只是渐进意义下的量级,并不能精确地对应算法的运行时间。有些非多项式时间算法,仍有可能在一部分实例上快速地完成求解。
如果某个算法的时间复杂度是关于输入数据中绝对值最大的数值的多项式量级,则称该算法为伪多项式时间算法。由于输入数据中的具体数值可以取到输入数据规模的指数量级,因此伪多项式时间算法并不一定是真正的多项式时间算法。例如,01 背包问题的动态规划算法是一个伪多项式时间算法,而非多项式时间算法。
当算法的最坏时间复杂度的发生概率较小时,平均意义下的时间耗用能够更加准确地度量算法的性能。算法在所有实例上的平均时间耗用,称为算法的平均时间复杂度。例如,快速排序算法的最坏时间复杂度为 \(O(n^2)\),平均时间复杂度则为 \(O(n \log n)\)。
某些算法会在输入数据上完成一系列的关联操作,如果对其中的每次操作都以最坏的情形来估计其耗时,可能会高估算法在该系列操作上的总体时间耗用。此时可以采用平摊分析方法,将该系列操作作为一个整体来估计其耗时,随后再将总体耗时平摊到每个操作上,以得到更为精准的分析结果。
如果某个问题存在多项式时间算法,则称该问题是一个 P(Polynomial)问题。对于某个问题,如果其解的正确性可以在多项式时间内完成验证,则称该问题是一个 NP(Nondeterministic Polynomial)问题。很显然,P 类问题同时也是 NP 类问题,即 P⊆NP。目前大多数研究人员倾向于认为 P≠NP,但是均无法给出证明。在目前未解决的问题中,P/NP 问题是最负盛名的数学难题之一,也是计算机科学的核心问题。
对于某个问题,如果所有的 NP 问题都可以多项式时间归约到该问题,则称其是 NP 难的(NP-hard)。如果某个问题不仅是 NP 问题,同时还是 NP 难的,则称其为 NP 完全(NP-Complete)问题。可以粗略地认为,NP 完全问题是 NP 问题中一类最难的问题:如果某个 NP 完全问题能够在多项式时间内解决,则所有的 NP 问题都将在多项式时间可解决。多数文献认为,可满足性问题(SAT)是第一个被证明的 NP 完全问题。
选择题:对于给定的 \(n\),分析以下代码段对应的时间复杂度,其中最为准确的时间复杂度为?
int i, j, k = 0;
for (int i = 0; i < n; i++) {for (int j = 1; j < n; j *= 2) {k = k + n / 2;}
}
- A. \(O(n)\)
- B. \(O(n \log n)\)
- C. \(O(n \sqrt{n})\)
- D. \(O(n^2)\)
答案
B。外层循环 \(O(n)\),内存循环 \(O(\log n)\)。
空间复杂度分析
算法的空间复杂度,指的是算法在整个执行过程中,所耗用的全部存储空间的量的峰值,一般表示成关于输入数据规模的某个函数。由于对算法耗用空间的精确计数往往难以实现,而且也没有特别重要的意义,因此在算法的空间复杂度分析中,常用大 O 记号来给出算法空间复杂度在渐进意义下的量级。
在算法的具体实现中,所耗用的存储空间不仅包括静态的存储空间,还包括动态申请的存储空间。因此,在分析有关的空间复杂度时,不仅要统计全局变量所耗用的存储空间,还要包括因函数或子程序调用而耗用的存储空间,其中包括局部变量等。复用的存储空间不需要被重复计入。
特别地,对于包含递归计算的算法,递归计算部分所耗用的存储空间的量与递归调用的深度相关。因此,应合理地控制递归调用的深度。
在存储空间资源比较宽松,但是时间效率要求较高的情况下,可以考虑采用“空间换时间”的策略,设置额外的空间来存储在整个算法执行过程中可能会多次计算的值,例如记忆化搜索等方法。这样可以避免一部分重复计算,以适当地增加存储空间为代价,有效地降低算法的时间耗用量,甚至降低算法的时间复杂度量级。
在时间效率要求不高,但是空间资源较为紧张的情形下,则可以考虑采用“时间换空间”的策略,尽可能地避免存储中间结果。对于需要多次使用的中间结果,每次都重新予以计算。这样就以适当地增加时间耗用量为代价,有效地降低算法的空间耗用量。
