线性规划是求一个线性函数在满足一组线性等式或不等式方程条件下极值的一类数学问题的统称。要求目标函数和约束方程必须是线性函数。隐含了如下假定:
比例性假定:决策变量的变化与资源消耗成比例;
可加性假定:每个决策变量的影响独立于其他变量;
连续性假定:决策变量可取连续值;
确定性假定:线性规划所有参数都是确定性参数,不含随机因素。
为什么要使用线性规划:
线性规划很容易而有效率地被求解;
如果存在最优解,则肯定能够找到;
功能强大的敏感性分析(sensitivity analysis);
许多实际问题本质上是线性的。
线性规划模型由三部分组成:
问题的目标--反映决策目标的目标函数,求其最大或最小值;
需要做什么决策,这些决策中间怎么约束的 a --一组线性等式、不等式约束方程;
需要做什么决策,这些决策中间怎么约束的 b --限制决策变量取值范围的非负约束。
构造线性规划模型需注意:
不是所有变量都需要出现在每一个约束中;
注意每个约束内参数量纲(单位)的一致性;
关于最优解,有几种情况:
无可行解(约束条件无交集);
有一个最优解(出现在角点);
有无数个最优解(目标函数与某个约束条件平行,这样当目标函数在角点处获得最优解时,在某个约束条件的线段上都会是最优解,从数学角度上说,就有无数个点=无数个解)。
使用EXCEL规划最优解时,常用到的几个函数有:
SUMPRODUCT函数:主要用于计算相乘后再相加的情况;
SUM函数:求和。
规划最优解示例1:
【问题】有8个小块和6 大块的玩具积木,要用这些材料去生产桌子和椅子。桌子需要2个大块+2个小块,椅子需要1个大块+2个小块。桌子可以卖20元,椅子可以卖15。问怎么组装,可以获得最大的利润?
【求解】设桌子有x个,椅子有y个。
1、目标函数就是 max(20x+15y);
2、约束函数就是:
1)2x+2y≤8;
2)x+2y≤6;
3)x,y ≥0.
3、建立excel,如果是offic的,就要加载宏“规范求解”;如果是WPS,就在数据--模拟分析--规划求解 这里使用规划求解功能。接下来分步骤进行:
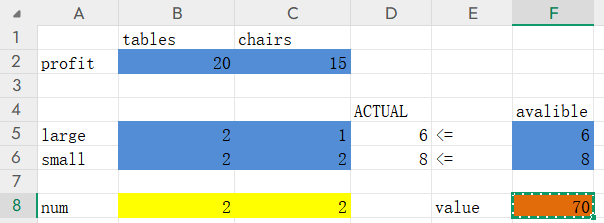
1)表格建立如下。其中,蓝色为数据;黄色是决策变量,空置;橙色是目标值,空置:
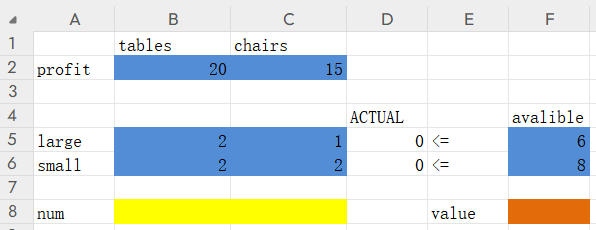
2)定义等式模型:
value是我们要求的目标值,就是最大利润,他的模型应该是:=SUMPRODUCT(B2:C2,B8:C8),也就是 20x+15y 在excel中对应cell的使用表达;
actual的D5和D6,模型为 =SUMPRODUCT(B5:C5,$B$8:$C$8)和==SUMPRODUCT(B6:C6,$B8:$C8),这里B8,C8有个$,是通过按 F4 ,使得这两个值变成固定值,这样配好了D5,直接拖拽下拉,只有B5C5会递增,B8C8不递增。这两个值其实就是x+2y和2x+2y在excell中对应cell的使用表达;
3)使用规划求解的宏,在excel 2007中,可在“数据--规划求解”,点击规划求解使用;使用WPS,可在“数据--模拟分析--规划求解”使用。我本地只有WPS,就只截图WPS。点击目标函数单元格 F8,然后点击规划求解。设置目标单元格、可变单元格和约束。这些都可以直接通过点击excel的具体格来操作,我这里截图做好的样子:
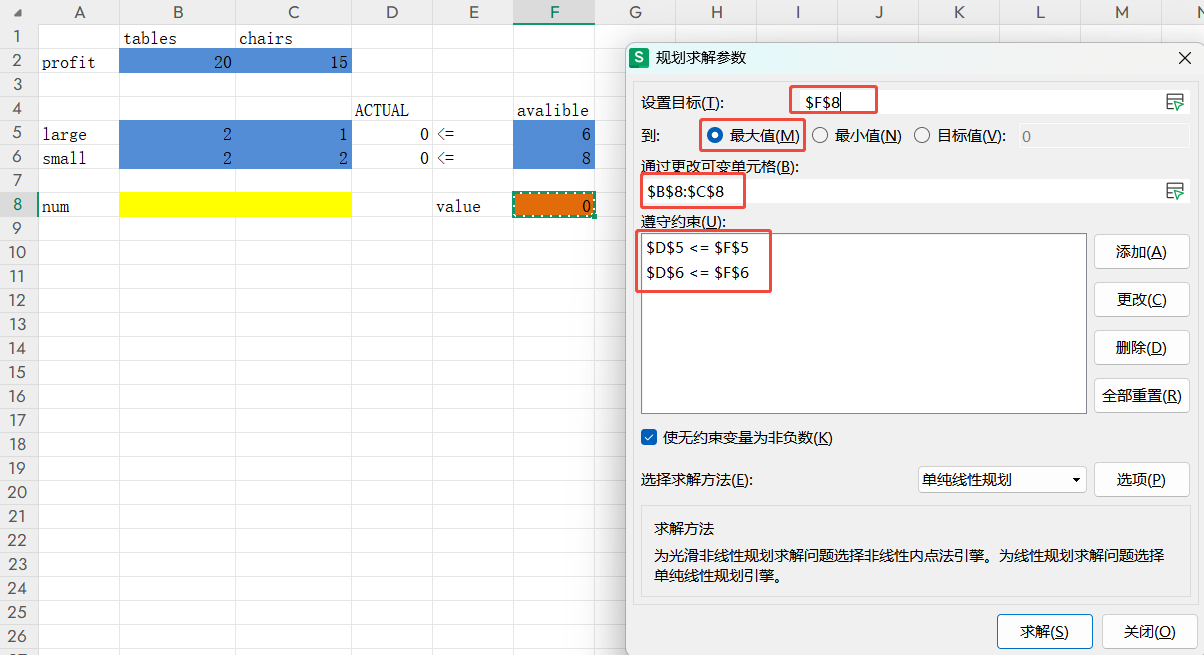
接下来,如果是excel,需要继续点击左边的选项,勾选“采用线性模型”和“假定非负”,来达到x,y≥0的约束。然后点确定,点求解。WPS注意就在当前页,勾选“使无约束变量为非负数”,然后点求解。答案如下,即,最优解为,做2个桌子,2个椅子,可获得最大利润70元: