题目内容
为了表彰小联为Samuel星球的探险所做出的贡献,小联被邀请参加Samuel星球近距离载人探险活动。 由于Samuel星球相当遥远,科学家们要在飞船中度过相当长的一段时间,小联提议用扑克牌打发长途旅行中的无聊时间。玩了几局之后,大家觉得单纯玩扑克牌对于像他们这样的高智商人才来说太简单了。有人提出了扑克牌的一种新的玩法。 对于扑克牌的一次洗牌是这样定义的,将一叠\(n\)(\(n\)为偶数)张扑克牌平均分成上下两叠,取下面一叠的第一张作为新的一叠的第一张,然后取上面一叠的第一张作为新的一叠的第二张,再取下面一叠的第二张作为新的一叠的第三张……如此交替直到所有的牌取完。 如果对一叠6张的扑克牌1 2 3 4 5 6,进行一次洗牌的过程如下图所示:
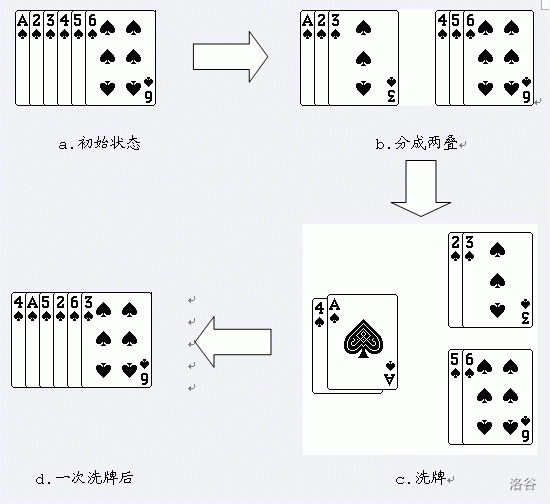
从图中可以看出经过一次洗牌,序列1 2 3 4 5 6变为4 1 5 2 6 3。当然,再对得到的序列进行一次洗牌,又会变为2 4 6 1 3 5。 游戏是这样的,如果给定长度为\(N\)的一叠扑克牌,并且牌面大小从1开始连续增加到\(n\)(不考虑花色),对这样的一叠扑克牌,进行\(m\)次洗牌。最先说出经过洗牌后的扑克牌序列中第\(l\)张扑克牌的牌面大小是多少的科学家得胜。小联想赢取游戏的胜利,你能帮助他吗?
其中\(0< l\le n \le 10 ^ {10}\) ,\(0 \le m \le 10^{10}\),且\(n\)为偶数。
解决方法
啊啊啊啊啊!!!都上太空了还在这里折磨人!!!
不过刚刚发现NKOJ的图床不能被别的网站调用。
我们充分利用观察力然后发现第\(x\)张牌在一次打乱后到\(f(x)\),则\(f(x)\)的表达式为:
\(x = \begin{cases}2x & (x\le n/2) \\2x-n-1 & (x>n/2)
\end{cases}\)
所以,我们可以看出,对于所有的\(x\),都有\(f(x)=2x\%(n+1)\)
也就是找到一个数\(ans\),即本题答案,使得\((ans\times 2^m)\%(n+1)=l\)
于是就可以用扩展欧几里得求出\(2^mx+y(n+1)=1\)的解,并且保证\(x\)是最小的非负整数。
再用\(x\)乘上\(l\)就可以得到\(ans\)
注意事项
由于\(m\)过大,所以你需要使用快速幂。
由于\(n\)和\(l\)过大(极限情况两数相乘可以达到\(10^{20}\)),你需要使用龟速乘或__int128(__int128不会,没试过,不知道)。
不要以为牌有周期性,压根没有的好吧。
代码
#include<bits/stdc++.h>
using namespace std;
#define int long long
int a,b,x,y,xx,y_,i1,i2,n,m,l,d,ans;
int c(int x,int y){//写法有点难看的龟速乘int a=0,q=x;while(y){if(y%2==1) a+=q,a%=(n+1);q+=q;q%=(n+1);y/=2;}return a%(n+1);
}
int po(int x,int y){//写法难看的快速幂int a=1,q=x;while(y){if(y%2==1) a=c(a,q),a%=(n+1);q=c(q,q);q%=(n+1);y/=2;}return a%(n+1);
}
void gcd(int a,int b){//写法十分难看的Exgcdif(b==0){x=1;y=0;return ;}gcd(b,a%b);xx=x;x=y;y=xx-a/b*y;// cout<<a<<" "<<b<<" "<<x<<" "<<y<<" "<<xx<<"\n";return ;
}
signed main()
{cin>>n>>m>>l;d=po(2,m);gcd(d,n+1);x%=(n+1);//68~70行,写法特别难看的取模x+=(n+1);x%=(n+1);ans=c(x,l)%(n+1);cout<<ans;//有同学问我为什么不特判ans=0,因为ans就等于不了0//如果ans=0,那么要么l=n+1或l=0(都不可能),要么x=0//如果x=0,那么说明n+1=1,不可能
}
