- A* 算法的核心思想
- A* 算法的三个关键公式
- 举例:走迷宫
- 总结
A* (A-Star) 算法是路径规划中非常经典、非常受欢迎的一种算法。对于初学者来说,我们可以把它想象成一个“聪明的寻路者”,它不像无头苍蝇一样乱撞,而是会有策略地寻找从起点到终点的最短路径。
A* 算法的核心思想
好的,没问题!A* (A-Star) 算法是路径规划中非常经典、非常受欢迎的一种算法。对于初学者来说,我们可以把它想象成一个“聪明的寻路者”,它不像无头苍蝇一样乱撞,而是会有策略地寻找从起点到终点的最短路径。
我们用一个非常简单的例子来理解它:在一个迷宫里找最短的出路。
A* 算法的核心思想
想象一下,你站在迷宫的起点,想要走到终点。每一步,你面前都有好几个路口可以选择。你会怎么选?
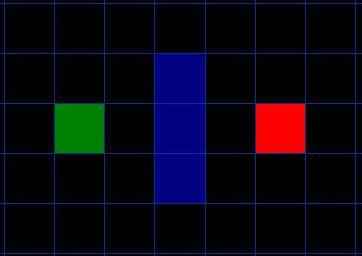
一个完全没有策略的人可能会随便选一条路走,走到死胡同再退回来,这叫深度优先搜索 (DFS),效率很低。
一个稍微聪明点的人可能会想:“我要把离我近的路口都先探一遍”,这就像水波纹一样从起点一圈圈扩散开来,直到找到终点。这叫广度优先搜索 (BFS) 或 Dijkstra 算法。
这种方法能保证找到最短路径,但它太“实诚”了,会探索很多明显错误的方向,比如离终点越来越远的路。
而 A* 算法是一个更聪明的寻路者,它在选择下一个要走的路口时,会同时考虑两个因素:
我已经付出的代价:从起点走到当前这个路口,我已经走了多远?G
我预估未来要付出的代价:从当前这个路口走到终点,大概还有多远? H
A* 算法的目标就是找到那个 “已付出代价” + “未来预估代价” 总和最小的路口,并把它作为下一步的选择。 这样就确保了它总是在最有希望的路径上进行探索。
A* 算法的三个关键公式
为了实现这个聪明的策略,A* 算法给每个格子(或节点)都赋予了三个值:G、H 和 F。
G 值:g(n) - 从起点到当前格子的实际代价
g(n) (g-score) 代表你从起点 A 走到当前格子 n 的确切移动成本。
在我们的迷宫例子里,假设每走一格的成本是 10,走斜线是 14 (模拟根号2),那么 g(n) 就是你从起点一路走过来累加的步数成本。
这个值是已知的、精确的
H 值:h(n) - 从当前格子到终点的预估代价(启发函数)
h(n) (h-score) 是一个估计值,它猜测从当前格子 n 走到终点 B 的最短距离大概是多少。这个值也被称为启发值 (Heuristic)。
这个估计不需要绝对精确,但必须是“乐观”的,也就是说,它永远不能高估实际的距离。
在网格地图中,最常用的计算方法是曼哈顿距离 (Manhattan Distance):忽略障碍物,只计算水平和竖直方向的总步数。h = (abs(当前格.x - 终点.x) + abs(当前格.y - 终点.y)) * 10
这个值是预估的、不一定精确的,它的作用是指引算法朝着终点的大方向前进。
F 值:f(n) - 总代价
f(n) (f-score) 是上面两个值的总和:
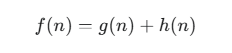
这个 F 值就是 A* 算法的决策依据。在所有待考察的格子里,F 值最低的那个,就是下一步最应该去探索的格子。
核心总结:回顾历史 + 展望未来
举例:走迷宫

步骤 1: 从起点开始
创建两个列表:
开启列表 (Open List):存放所有待考察的格子。
关闭列表 (Closed List):存放所有已经考察过的、不会再去的格子。
将起点 A 放入 开启列表。
步骤 2: 第一次寻路
从 开启列表 中找到 F 值最低的格子。现在只有起点 A,所以就是它了。
将 A 从 开启列表 移到 关闭列表。
查看 A 周围所有可以走且不在关闭列表中的邻居格子(图中蓝色高亮的格子)。
为每个邻居格子计算 G、H、F 值,并将它们放入 开启列表。同时,记录它们的“父节点”是 A(这样我们最后才能追溯路径)。
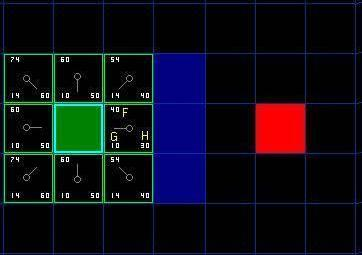
步骤 3: 第二次寻路
从 开启列表 中选择 F 值最低的格子。我们有1个 F=40 的格子,我们称它为 C。
将 C 从 开启列表 移到 关闭列表。
查看 C 的所有邻居(不包括墙和已在关闭列表中的 A)。
把C当成是这些新加入邻居的父亲,
如果某个邻居已经在open_list中,检查这条路径是否更优,经由当前方格到达这个邻居的G值 比邻居的G值如果更小,那么就把当前点设定为那个邻居点的父亲,并更新邻居点的GHF
步骤 4: 持续循环
算法会不断重复这个过程:
从开启列表中取出 F 值最低的格子。
把它移到关闭列表。
把它所有合格的邻居加入开启列表。
我们继续往下走,你会发现算法会优先探索 F 值更低的格子。比如,当路径遇到墙壁需要绕路时,绕路格子的 G 值会变大,导致 F 值也变大,算法就会暂时放弃这个方向,转而探索其他 F 值更低(更有希望)的格子。
步骤 5: 找到终点
当终点 B 被加入到 开启列表 时,就意味着我们找到了一条路径!
但是,这不一定是最佳路径。算法的结束条件是:当要从开启列表中取出的 F 值最低的节点正好是终点 B 时,搜索结束。
此时,我们就可以从终点 B 开始,通过每个格子记录的“父节点”信息,一步步反向追溯到起点 A。这条追溯出来的路径,就是 A* 算法找到的最短路径。
总结
A* = Dijkstra + Heuristic:你可以把 A* 理解为在 Dijkstra 算法(保证最短)的基础上,增加了一个启发函数 H(提供方向感),使得搜索更加高效。
开启列表 (Open List):一个“待考察”的候选列表,按 F 值排序,总是优先处理最有希望的节点。
关闭列表 (Closed List):一个“黑名单”,记录所有已经处理过的节点,防止重复计算和走回头路。
F = G + H 是算法的精髓:
G 值让算法倾向于选择更短的已知路径。
H 值让算法倾向于朝着终点方向前进。
