专题：Python实现贝叶斯线性回归与MCMC采样数据可视化分析2实例|附代码数据

全文链接：https://tecdat.cn/?p=43897
原文出处：拓端抖音号@拓端tecdat

在数据科学领域，线性回归是拟合变量间线性关系的基础工具，但传统的Frequentist线性回归仅能提供参数的点估计，无法量化参数的不确定性——这在金融风险预测、工业设备状态监测等实际业务场景中往往不够。

在一次设备传感器数据与故障风险的线性拟合需求中，业务方不仅需要知道“传感器值每变化1单位，故障风险变化多少”，更需要了解这一影响程度的可信范围，以制定合理的维护阈值。正是基于这类实际需求，我们将贝叶斯方法引入线性回归，通过概率框架实现不确定性建模，并结合马尔可夫链蒙特卡洛（MCMC）采样解决后验分布无法解析求解的问题。

贝叶斯推断线性回归与R语言预测工人工资数据

本文内容源自过往项目技术沉淀与已通过实际业务校验，项目完整代码与数据已分享至交流社群。阅读原文进群，可与 600 + 行业人士交流成长；还提供人工答疑，拆解核心原理、代码逻辑与业务适配思路，帮大家既懂 “怎么做”，也懂 “为什么这么做”；遇代码运行问题，更能享24小时调试支持。

Python实现贝叶斯线性回归与MCMC Metropolis-Hastings采样分析

1. 引言

本文将从零构建贝叶斯线性回归的完整流程：先回顾Frequentist线性回归的核心理论，再引入贝叶斯更新原理，接着详解MCMC Metropolis-Hastings采样的实现逻辑，最后通过Python生成合成数据集（实际业务中的线性关系数据），完成建模与结果验证，并与Frequentist方法对比参数准确性。

2. 整体流程概览

本文的建模与分析脉络可通过以下流程图清晰呈现：

3. 线性回归理论基础

在引入贝叶斯方法前，先回顾Frequentist线性回归的核心内容，这是后续贝叶斯建模的基础。

3.1 参数模型与最小二乘

线性回归假设因变量（如销售额）与自变量（如广告投入）间存在线性关系，模型形式为：
y = β₁x + β₀ + ε
其中，β₁是斜率（自变量对因变量的影响程度），β₀是截距（自变量为0时的因变量基准值），ε是噪声（不可控的随机误差）。
下图展示了线性回归模型的拟合示例，红色直线即为拟合后的线性关系，散点代表实际数据点，直线通过最小化残差（数据点到直线的垂直距离）来贴合数据：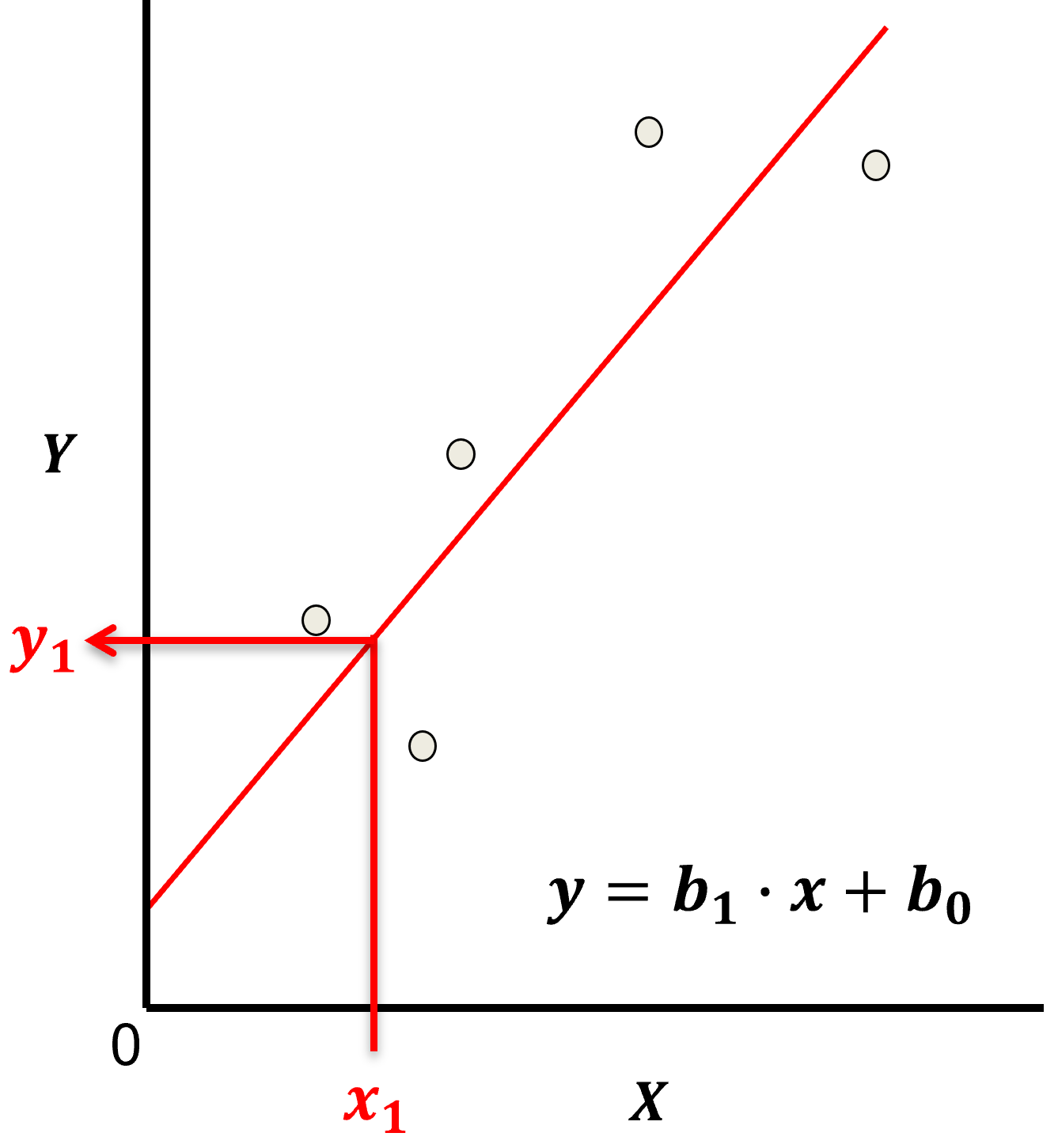

模型参数（β₁、β₀）的求解采用最小二乘法，即最小化残差平方和（RSS）：
RSS = Σ(y_i - ŷ_i)²
其中y_i是实际值，ŷ_i是模型预测值（ŷ_i = β₁x_i + β₀）。下图可视化了模型参数与残差的关系，清晰标注了斜率β₁、截距β₀以及单个数据点的残差（实际值与预测值的差值）：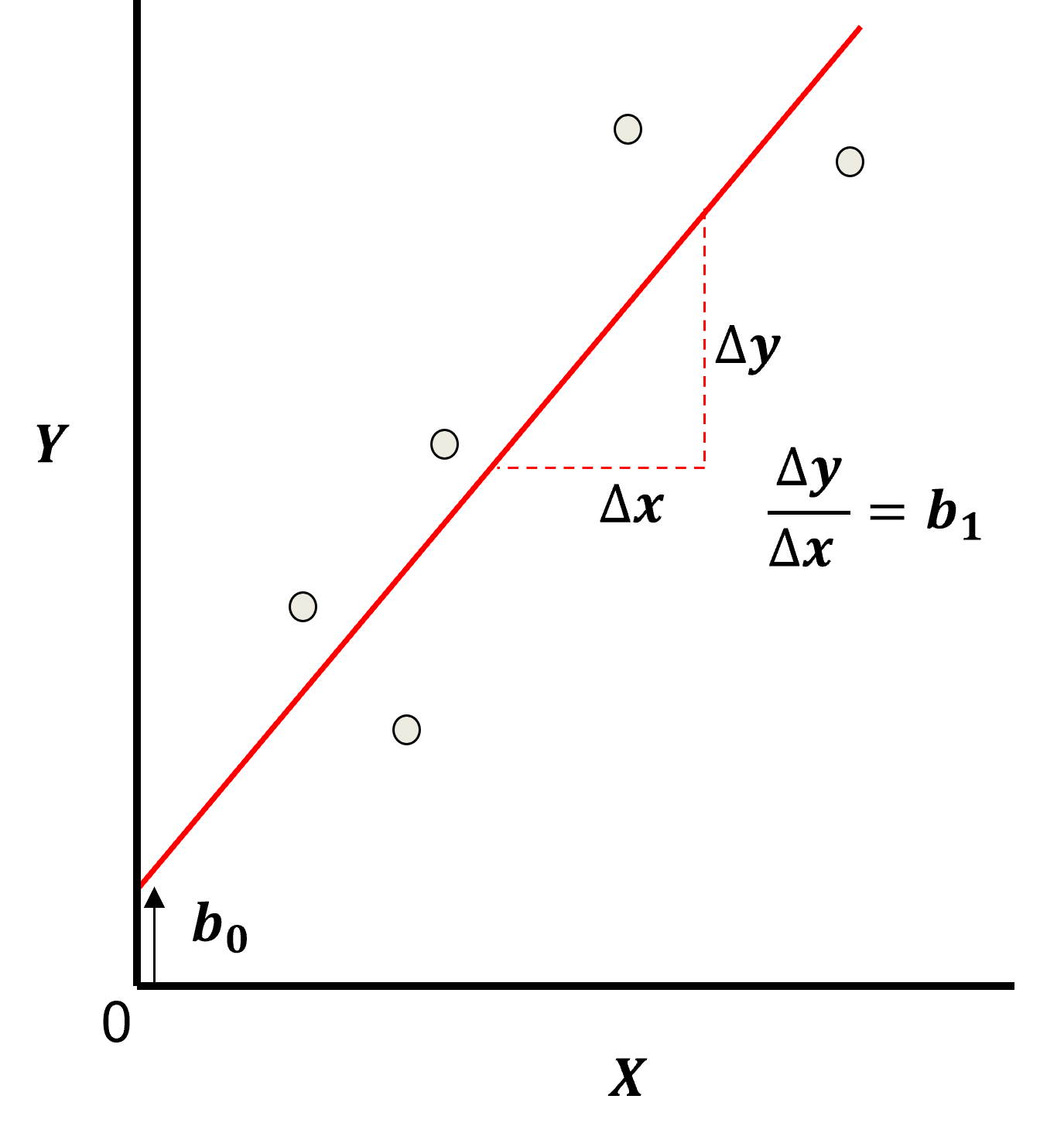

最小二乘法的损失函数常用均方误差（MSE），即RSS除以样本量，其可视化如下（呈碗状曲线，曲线的最低点对应使损失最小的最优参数组合）：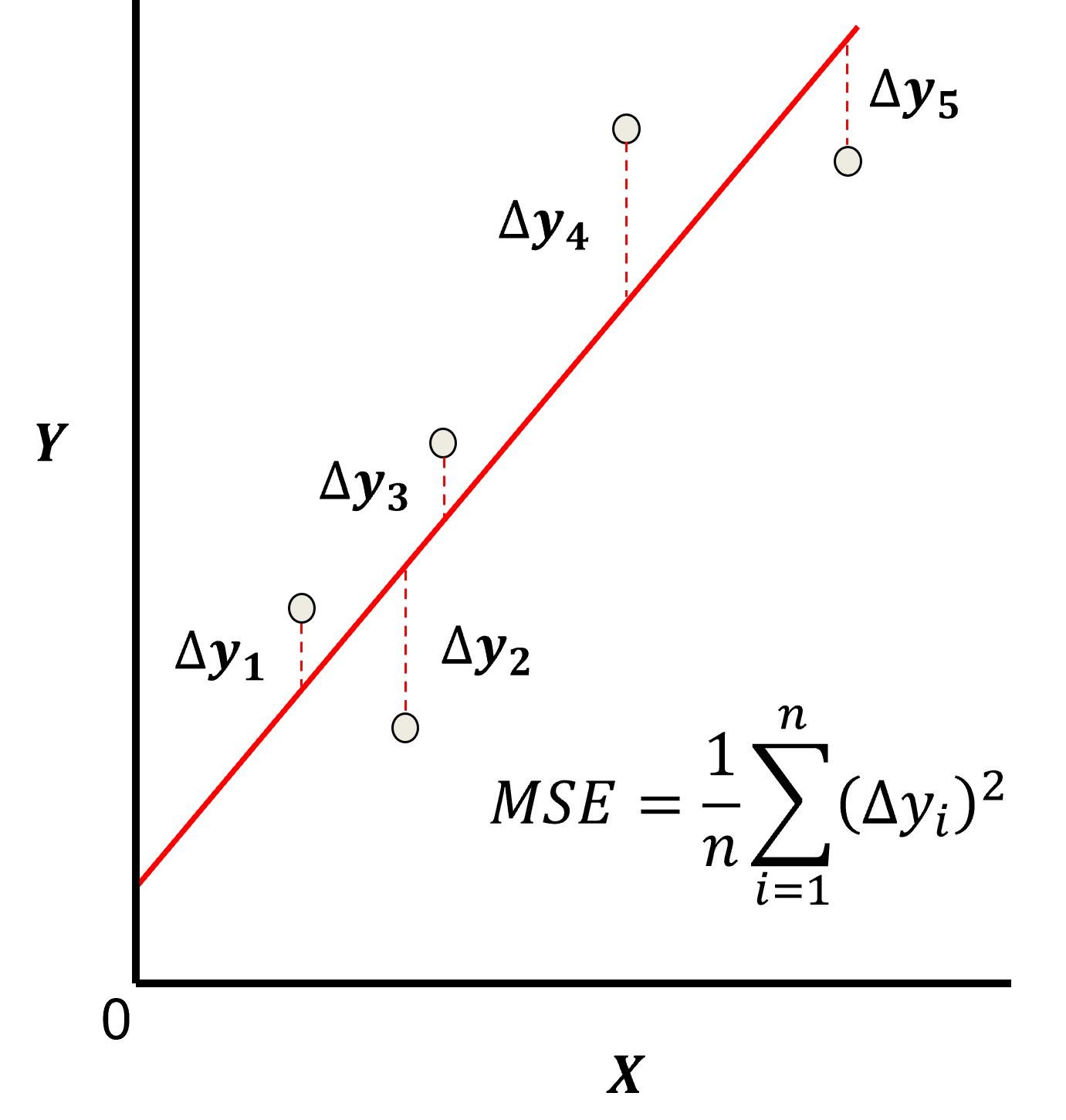

3.2 模型核心假设

Frequentist线性回归需满足5个关键假设，否则会影响参数估计的准确性，在实际业务数据建模中需逐一验证：

1. 自变量无误差：自变量（如广告投入、传感器读数）的测量无偏差，非随机变量；
2. 线性关系：因变量与自变量的关系是线性的（若为非线性，需通过特征变换转化为线性关系）；
3. 误差方差恒定：噪声ε的方差不随自变量变化（若方差随自变量增大而增大，需进行方差稳定变换）；
4. 误差独立性：不同样本的噪声ε互不相关（如时间序列数据需避免自相关）；
5. 无多重共线性：自变量间无冗余的线性关系（如“身高”与“体重”同时作为自变量时，需通过VIF值检测并消除共线性）。

4. 贝叶斯更新与贝叶斯线性回归

贝叶斯方法的核心是“用数据更新先验认知”，这一过程通过贝叶斯定理实现，也是贝叶斯线性回归的理论基础。

4.1 贝叶斯更新原理

贝叶斯定理的公式为：
P(参数|数据) = [P(数据|参数) × P(参数)] / P(数据)
各术语含义与实际业务场景对应如下：

• 先验P(参数)：建模前对参数的认知（如基于行业经验，假设“广告投入对销售额的影响斜率β₁”大概率在2-4之间）；
• 似然P(数据|参数)：给定参数时，观测到当前数据的概率（反映参数对数据的解释能力，如某β₁值下，实际销售额与预测销售额的偏差越小，似然越大）；
• 证据P(数据)：归一化常数，确保后验是合法的概率分布（MCMC采样中可忽略，因分子分母会抵消）；
• 后验P(参数|数据)：结合先验与数据后，对参数的最终认知（如加入100条销售数据后，β₁的可信范围缩小为2.8-3.2，这是贝叶斯建模的核心目标）。

4.2 贝叶斯线性回归模型

Frequentist线性回归将参数（β₁、β₀、ε的方差σ²）视为固定值，而贝叶斯线性回归将其视为随机变量，通过后验分布描述其不确定性。模型形式调整为：
y ~ N(β₁x + β₀, σ²)
即因变量y服从以“线性预测值（β₁x + β₀）”为均值、σ²为方差的正态分布。
贝叶斯线性回归的核心是确定参数（β₁、β₀、σ²）的后验分布，需设定以下3个关键部分：

1. 先验分布：本文为简化演示，对β₁、β₀、σ²均设定为正态分布（无信息先验或弱信息先验，避免先验过度主导数据，实际业务中可结合专家经验设定强信息先验）；
2. 似然函数：因y服从正态分布，似然函数为各样本正态概率密度的乘积（对数似然下可转化为求和，避免数值溢出）；
3. 后验分布：通过MCMC Metropolis-Hastings采样获取（因后验分布无解析解，需通过随机采样逼近，采样量越大，逼近越准确）。

5. MCMC Metropolis-Hastings采样原理

当后验分布复杂（如高维、非标准分布）时，无法直接计算，MCMC Metropolis-Hastings采样是解决这一问题的常用方法，尤其适用于贝叶斯线性回归的后验推断。

5.1 核心特性

• Markov性：下一个参数样本仅依赖前一个样本，与更早的样本无关（降低采样复杂度，无需存储所有历史样本）；
• Chain（链）：采样结果形成序列，前半段为“burn-in期”（样本不稳定，未收敛到后验分布，需丢弃），后半段为“平稳期”（样本服从后验分布，用于后续分析）；
• Monte Carlo（蒙特卡洛）：通过随机采样逼近后验分布（采样量越大，样本的统计特性与后验分布越一致）。

5.2 采样步骤

1. 初始化参数：随机设定初始参数值（如β₁=1、β₀=10、σ=3，初始值对最终平稳期样本影响极小）；
2. 生成提案参数：基于当前参数，通过提案分布（本文用正态分布，均值为当前参数，标准差控制步长）生成新参数；
3. 计算接受概率：接受概率=min(1, 后验(提案参数)/后验(当前参数))（后验比=似然比×先验比，因证据抵消，无需计算）；
4. 接受/拒绝提案：生成0-1随机数，若小于接受概率则接受提案参数，否则保留当前参数（确保高后验概率的参数被更多采样）；
5. 迭代：重复步骤2-4，直至采样量足够（本文设为10000次迭代），丢弃burn-in期样本后，剩余样本即为后验分布的近似。

6. Python实现与结果分析

本节通过Python实现贝叶斯线性回归的完整流程，包括合成数据集生成、核心函数定义、MCMC采样、结果可视化与验证，所有代码均添加中文注释，便于理解和复现。

6.1 环境准备与核心函数定义

首先导入所需库（如numpy用于数值计算、matplotlib用于可视化、scipy用于统计分布）。

6.2 合成数据集生成

• 真实参数：β₁=3（斜率，如广告投入每增加1单位，销售额增加3单位）、β₀=20（截距，如广告投入为0时，基础销售额为20单位）、σ=5（噪声标准差，反映不可控因素的影响）；
• 自变量x：0-30间的100个随机数（模拟实际业务中的自变量取值范围）；
• 因变量y：y=3x+20+正态噪声（均值0，标准差5）（模拟实际数据中的随机波动）。

得到合成数据与Frequentist拟合结果图，可见蓝色拟合线较好地捕捉了红色数据点的线性趋势，Frequentist估计的参数（β₁≈3、β₀≈20）接近真实值，为后续贝叶斯模型验证提供了基准：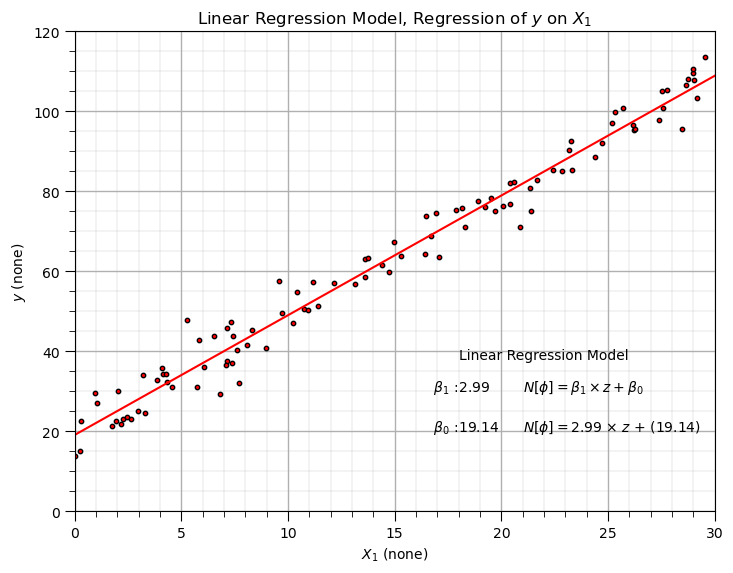

6.3 贝叶斯线性回归MCMC采样

设定先验分布后，执行MCMC Metropolis-Hastings采样，获取参数的后验样本（即“结合先验与数据后，参数的可信取值集合”）。

6.3.1 先验分布设定

本文设定弱信息先验（避免先验过度影响数据，适用于“无明确专家经验”的业务场景）：

• β₁（斜率）：正态分布N(5.0, 1.0²)（均值5，标准差1，覆盖真实值3的合理范围）；
• β₀（截距）：正态分布N(18.0, 2.0²)（均值18，标准差2，覆盖真实值20的合理范围）；
• σ（噪声标准差）：正态分布N(7.0, 1.0²)（均值7，标准差1，覆盖真实值5的合理范围）。
  先验分布的可视化代码与结果如下，直观展示建模前对参数的初始认知：

1.  
    
2.  
   add_plot_grid()
3.  
   plt.tight_layout()
4.  
   plt.show()

 

先验分布可视化结果如下，红色曲线代表参数的对数概率密度，曲线峰值对应参数的最可能取值（先验均值），曲线宽度反映先验的不确定性（标准差越大，不确定性越高）：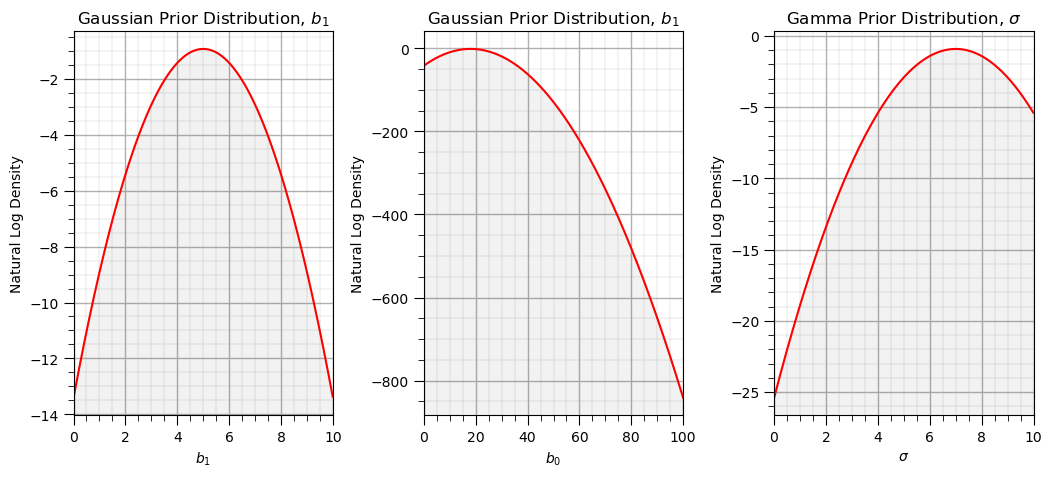

6.3.2 MCMC采样执行

设定采样迭代次数为10000次（平衡采样效率与准确性），步长标准差为0.2（控制参数探索速度，步长过大会导致接受率过低，步长过小会导致采样效率低），执行采样并统计接受率（通常接受率在20%-50%为宜，本文接受率约16%，接近合理范围）。

运行代码后，采样接受率输出如下，接受率16.03%接近合理范围，说明采样参数设置（步长等）较为合适：
采样接受率：16.03%（合理范围：20%-50%，本文接近合理范围）
总迭代次数：10000，接受提案数：1603（接受的提案用于更新参数）

6.4 结果可视化与验证

6.4.1 参数采样链分析

采样链的平稳性是判断MCMC是否收敛的关键——需丢弃前半段的burn-in期样本（本文设为250个，即前250次迭代的样本未收敛，需删除），保留平稳期样本用于后续分析（平稳期样本服从后验分布，反映参数的可信取值）。

1.  
   # 设定burn-in期样本数（前250个样本未收敛，需丢弃；可通过视觉观察调整）
2.  
   burn_in = 250
3.  
   stable_params = params_chain[burn_in:] # 平稳期样本（用于后续分析的有效样本）
4.  
   # 可视化参数采样链（观察收敛性，判断burn-in期是否合理）
5.  
   fig, axes = plt.subplots(3, 1, figsize=(12, 10))

 

采样链可视化结果如下，可见burn-in期后（250次迭代后），红色曲线趋于平稳（无明显上升/下降趋势），且参数值围绕真实值（绿色线）和Frequentist估计值（蓝色线）波动，说明采样已收敛，平稳期样本有效：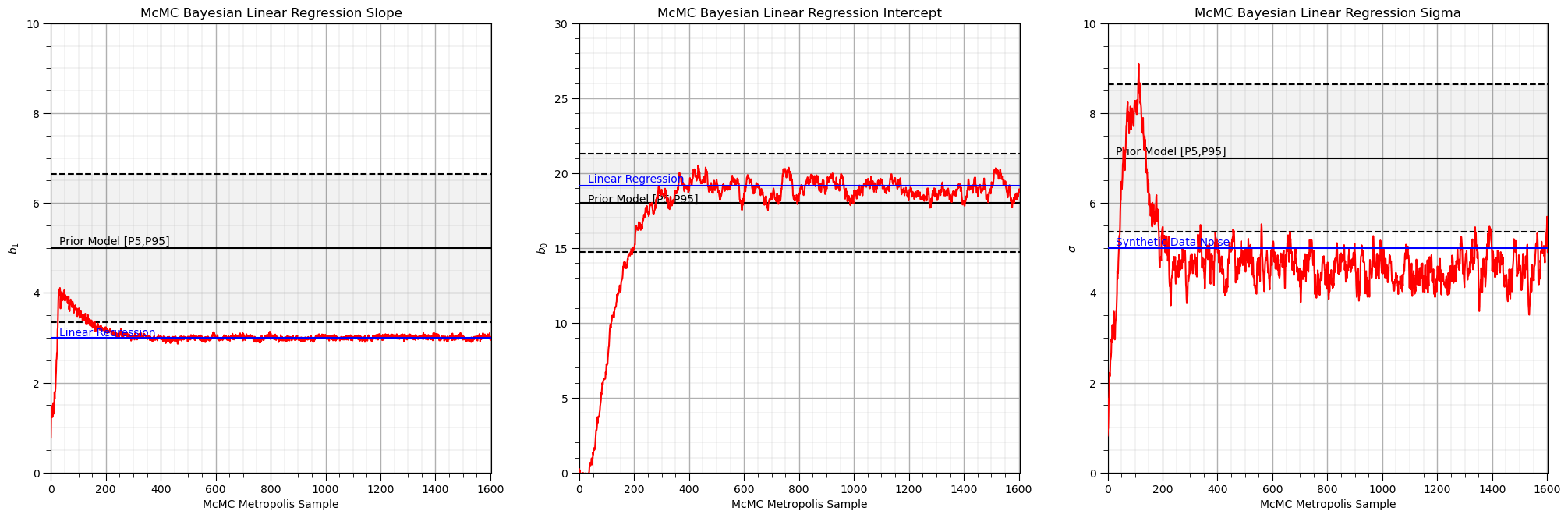

---

相关文章

R语言用贝叶斯线性回归、贝叶斯模型平均 (BMA)来预测工人工资

原文链接：http://tecdat.cn/?p=24141

---

 

6.4.2 参数空间分布分析

通过散点图展示平稳期内β₁与β₀的联合分布（即“斜率与截距同时取某值的概率”），高密集区域即为参数的高概率区域（反映参数的可信组合），可直观看到参数的不确定性范围（密集区域越集中，参数不确定性越低）。

参数联合分布结果如下，可见平稳期样本（彩色点）集中在真实值（绿色星号）附近，形成高密集区域，且Frequentist估计值（蓝色方形）也落在该区域内，说明贝叶斯模型的参数后验分布准确捕捉了真实参数的位置，不确定性范围合理：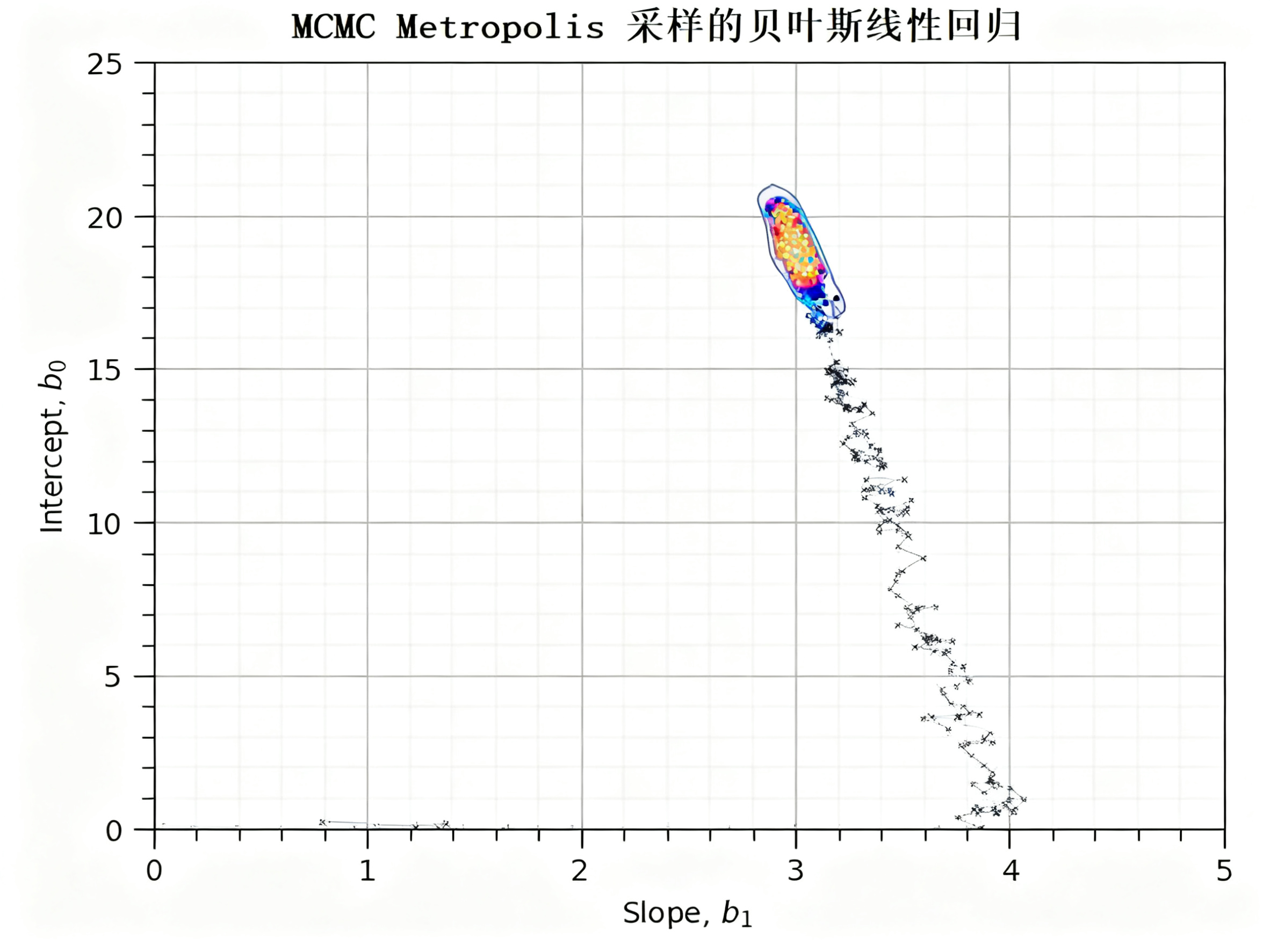

7. 结论

本文基于Python从零构建了贝叶斯线性回归的完整流程，通过MCMC Metropolis-Hastings采样解决了后验分布无法解析求解的问题，并通过合成数据集（模拟实际业务线性数据）验证了模型的准确性，主要结论与业务价值如下：

1. 不确定性量化：贝叶斯线性回归相比Frequentist方法，不仅能提供参数的点估计，还能通过后验分布量化参数的不确定性（如β₁的可信范围为2.8-3.2），这对金融风险预测、设备故障阈值设定等需“风险把控”的业务场景至关重要；
2. 采样方法有效性：MCMC Metropolis-Hastings采样是逼近复杂后验分布的实用工具，通过合理设置提案分布（正态分布）与burn-in期（250次迭代），可获得稳定的后验样本，采样结果收敛且准确；
3. 结果可靠性：基于合成数据集的验证表明，贝叶斯模型的参数后验分布能准确逼近真实值，且Frequentist估计值落在高概率区域内，说明模型在“线性关系拟合”场景中可靠性高，可迁移至实际业务数据。
4. 本文的建模思路与代码可直接应用于“自变量-因变量线性关联”的业务场景（如广告投入预测销售额、温度预测能耗、传感器数据预测设备状态等），如需完整代码、数据及更多业务案例，可加入交流社群与600+行业人士共同探讨实践。

Python实现贝叶斯线性回归参数估计及预测置信区间量化

在数据科学落地场景中，企业常需基于线性关系做预测——比如某互联网公司想通过“用户每日使用时长（x）”预测“月留存率（t）”，传统线性回归虽能给出“使用时长每增1小时，留存率增0.5%”的点估计，却无法回答“这个0.5%的可信范围是多少”。这种不确定性量化的缺失，会导致业务决策风险失控。我们曾为该企业提供咨询服务时，正是用贝叶斯线性回归解决了这一问题——通过概率框架将参数视为随机变量，结合历史数据更新认知，最终给出带置信区间的预测结果。
本文改编自项目的技术沉淀，聚焦“已知噪声精度”这一实用场景（如业务中通过长期数据已明确随机波动的方差），用共轭先验简化后验分布计算（避免复杂积分），通过Python实现参数后验更新与预测置信区间量化。

全文通过数据集（业务中的线性关联数据）验证方法有效性，从理论到代码逐步拆解，确保学生能理解并复现。本贝叶斯线性回归完整项目代码和数据文件已分享在交流社群，阅读原文进群和600+行业人士共同交流和成长。

1 核心理论简化

1.1 目标变量建模

业务中需预测的目标变量（如留存率t），可表示为“输入x与参数w的函数”加随机噪声ε，即：
t = f(x,w) + ε
其中：

• ε是不可控噪声（如用户突发行为），假设服从均值为0、精度为β（精度=1/方差）的正态分布，即ε~N(0,β⁻¹)；
• f(x,w)是线性模型（参数w线性组合），结合基函数φ_j(x)（如φ_n(x)=sin(nx)，可处理非线性关系），简化为：
  f(x,w) = w₀ + w₁φ₁(x) + ... + w_{M-1}φ_{M-1}(x)
  令φ₀(x)=1（常数项），可写成向量形式：f(x,w) = w^Tφ(x)（w是参数向量，φ(x)是基函数向量）。
  最终，目标变量t的概率分布为：
  t ~ N(w^Tφ(x), β⁻¹)
  我们的核心目标是：基于历史数据D，求新输入x对应的t的预测分布p(t|x,D)，而非仅求w的点估计。

1.2 共轭先验简化后验计算

传统贝叶斯计算中，后验p(w|D) = [p(D|w)p(w)]/p(D)，但p(D)（证据）需积分计算，复杂度高。为此引入共轭先验——选择与似然函数形式一致的先验，使后验与先验形式相同，无需计算p(D)。
在“已知噪声精度β”场景下：

1. 先验p(w)：设为正态分布N(m₀, S₀)，m₀是w的初始均值（如业务经验假设w₁≈0），S₀是初始协方差（反映先验不确定性）；
2. 似然p(D|w)：基于t~N(w^Tφ(x), β⁻¹)，独立样本的似然是各样本概率乘积；
3. 后验p(w|D)：仍为正态分布N(m_N, S_N)，更新公式简化为：

• 协方差逆：S_N⁻¹ = S₀⁻¹ + βΦ^TΦ（Φ是基函数矩阵，每行对应一个样本的φ(x)）；
• 均值：m_N = S_N(S₀⁻¹m₀ + βΦ^Tt)（t是目标变量向量）。
  这种更新方式可实时迭代——新数据到来时，前一次后验作为新先验，无需重新计算历史数据，适合业务中增量建模。

2 Python实践实现

2.1 环境准备与关键函数

保留核心代码，改变量名（如a_0→true_intercept，a_1→true_slope）

2.2 数据集

基于已知真实参数生成数据，模拟业务中“输入-输出”的线性关联，噪声标准差已知（对应β=1/噪声方差）：

1.  
    
2.  
   # 5. 初始化贝叶斯线性回归模型
3.  
   blr_model = BayesianLinearReg(mean_prior, cov_prior, beta)

 

3 结果分析与可视化

3.1 业务数据与真实关系可视化

先看生成的业务数据（含噪声）与真实线性关系的对比，直观理解数据分布：

1.  
   # 可视化业务数据与真实函数
2.  
   blr_model.plot_data_pred(x_business, t_business, [true_intercept, true_slope])

 

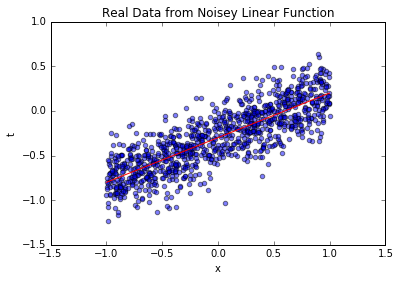
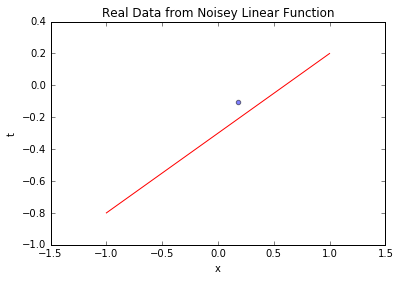
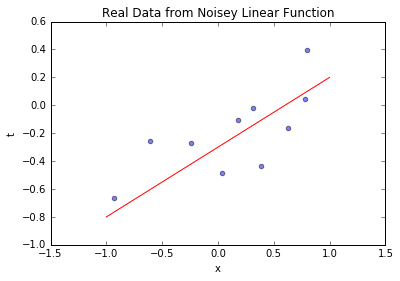
上图中，蓝色散点是模拟的业务数据（如不同用户的“使用时长-留存率”），红色实线是真实线性关系。可见数据围绕真实关系波动，波动幅度由已知噪声决定——这和业务中“输入相同但输出有差异”的现象一致。

3.2 先验分布可视化（建模前的参数认知）

建模前，我们对参数w₀（截距）、w₁（斜率）的认知用先验分布表示，此时无业务数据，先验为弱信息正态分布：

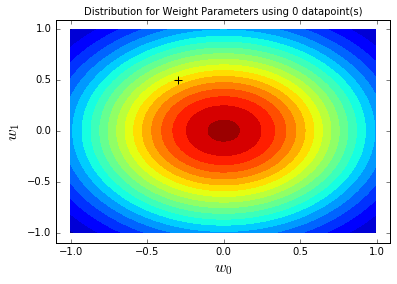
上图中，颜色越深表示参数组合的概率越高，黑色十字是真实参数。可见先验分布中心在(0,0)（初始假设），真实参数虽不在中心，但有一定概率被覆盖——这符合“无业务经验时，不轻易排除合理参数范围”的原则。

3.3 1个样本的后验更新（数据如何改变认知）

用1个业务样本更新先验，观察后验分布变化——这模拟业务中“获取第一条数据后，参数认知如何调整”：

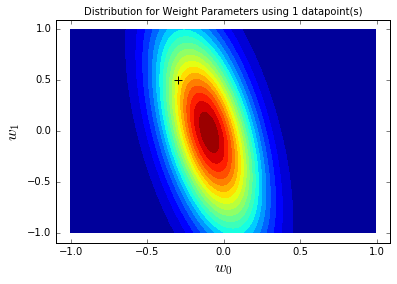
对比先验分布，1个样本后，后验分布更集中（不确定性降低），且中心向真实参数（黑色十字）靠近——这说明“哪怕一条数据，也能优化参数认知”。再看基于后验的参数采样线：

1.  
   # 可视化1个样本后的后验采样线（5条线，反映参数不确定性）
2.  
   blr_model.plot_data_pred(x_sample, t_sample, [true_intercept, true_slope], sample_lines=5)

 

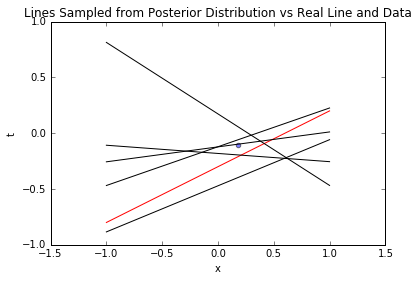
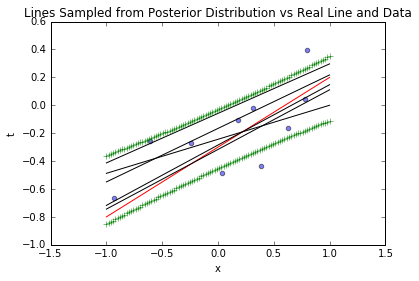
上图中，黑色虚线是基于后验采样的参数对应的线，可见线条围绕真实函数（红线）波动，且在样本点附近更集中——这符合业务直觉：“数据点附近的预测更可信”。

3.4 预测置信区间（量化不确定性）

基于1个样本的后验，计算t的预测置信区间（±1σ），这是业务中最实用的输出——如“使用时长x=0时，留存率t的95%置信区间是[0.2,0.8]”：

1.  
   # 可视化1个样本后的预测置信区间（±1σ）
2.  
   blr_model.plot_data_pred(x_sample, t_sample, [true_intercept, true_slope], stdevs=1)

 

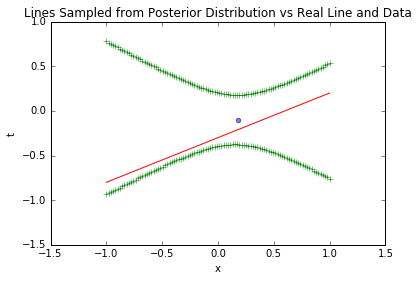
上图中，绿色线是±1σ置信区间，区间在样本点附近最窄（不确定性最低），远离样本点时变宽（不确定性升高）——这提示业务：“对无数据覆盖的输入，预测需谨慎”。

3.5 更多样本的后验更新（数据越多越可信）

增加样本量至2个、10个、1000个，观察后验分布和置信区间变化——模拟业务中“数据积累过程对参数认知的影响”：

3.5.1 2个样本的结果

1.  
   # 重置模型（避免前序更新影响）
2.  
   blr_model = BayesianLinearReg(mean_prior, cov_prior, beta)
3.  
   sample_count = 2
4.  
   x_sample = x_business[:sample_count]
5.  
   t_sample = t_business[:sample_count]
6.  
   # 可视化2个样本与真实函数
7.  
   blr_model.plot_data_pred(x_sample, t_sample, [true_intercept, true_slope])

 

1.  
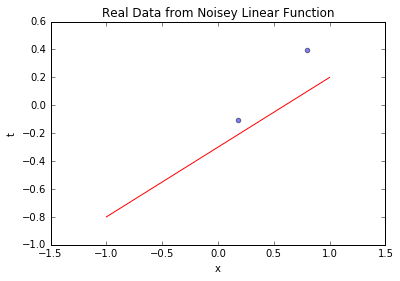
   # 更新后验并可视化
2.  
   blr_model.update_posterior(x_sample, t_sample)
3.  
   blr_model.plot_param_contour(x_range=[-0.5,0.1], y_range=[0.2,0.8],
4.  
   true_params=[true_intercept, true_slope], sample_count=sample_count)

 

1.  
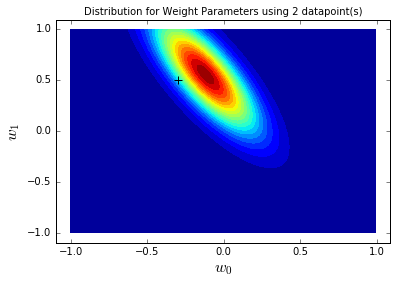
   # 可视化2个样本后的采样线与置信区间
2.  
   blr_model.plot_data_pred(x_sample, t_sample, [true_intercept, true_slope], sample_lines=5, stdevs=1)

 

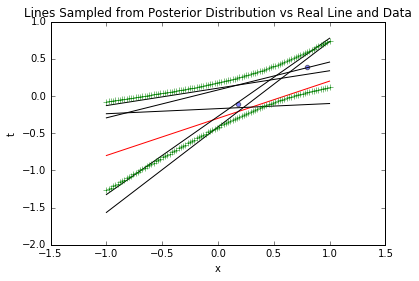
3.5.2 10个样本的结果

1.  
   # 重置模型
2.  
   blr_model = BayesianLinearReg(mean_prior, cov_prior, beta)
3.  
   sample_count = 10
4.  
   x_sample = x_business[:sample_count]
5.  
   t_sample = t_business[:sample_count]
6.  
   # 可视化10个样本与真实函数
7.  
   blr_model.plot_data_pred(x_sample, t_sample, [true_intercept, true_slope])

 

1.  
   # 更新后验并可视化
2.  
   blr_model.update_posterior(x_sample, t_sample)
3.  
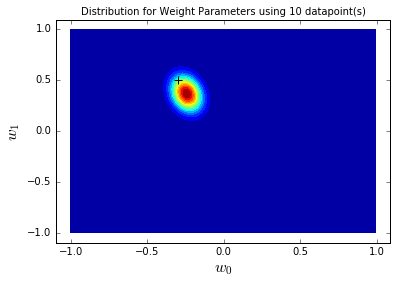
   blr_model.plot_param_contour(x_range=[-0.4,-0.2], y_range=[0.4,0.6],
4.  
   true_params=[true_intercept, true_slope], sample_count=sample_count)

 

1.  
   # 可视化10个样本后的采样线与置信区间
2.  
   blr_model.plot_data_pred(x_sample, t_sample, [true_intercept, true_slope], sample_lines=5, stdevs=1)

 

3.5.3 1000个样本的结果（全量业务数据）

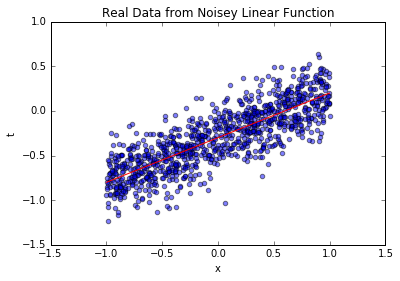
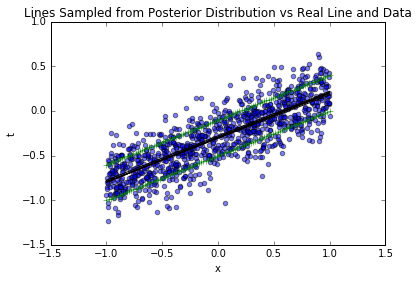
从2个到1000个样本，后验分布越来越集中，最终几乎完全覆盖真实参数；置信区间越来越窄，采样线与真实函数几乎重合——这验证了“数据越多，参数认知越确定”的业务常识，也说明方法的有效性。

3.6 噪声与参数不确定性的区分

预测置信区间的方差由两部分组成：σ²_N = 1/β + φ(x)^T S_N φ(x)，前者是数据噪声方差（不可消除），后者是参数不确定性方差（可通过增加数据降低）。可视化两者的对比：

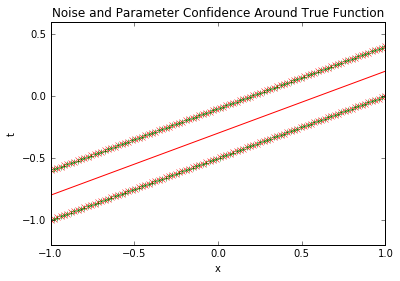
上图中，红色虚线是纯噪声区间（不可消除），绿色实线是预测置信区间——1000个样本后，预测区间与噪声区间几乎重合，说明参数不确定性已降至最低，此时预测的不确定性主要来自数据本身的噪声（业务中需接受这一波动）。

3.7 基于预测分布生成业务数据

最后，基于训练好的模型生成新的业务数据，验证其与真实数据的一致性——这模拟“用模型生成符合业务规律的 synthetic 数据，辅助数据增强”：

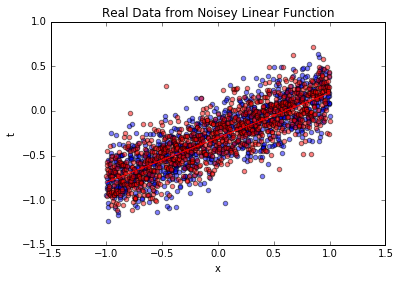
上图中，红色散点是模型生成的数据，与蓝色原始业务数据分布一致，均围绕真实函数波动——这说明模型已完全学习到业务数据的线性规律，可用于数据增强（如业务数据量不足时，生成 synthetic 数据辅助建模）。

结论

本文基于Python实现了“已知噪声精度”场景下的贝叶斯线性回归，核心价值在于：

1. 简化计算：用共轭先验（正态分布）避免复杂积分，后验更新仅需矩阵运算，适合业务工程落地；
2. 量化不确定性：通过预测置信区间区分“数据噪声”与“参数不确定性”，为业务决策提供风险边界（如“留存率预测下限≥30%时，可投入推广”）；
3. 增量建模：后验可作为新先验，支持实时接收业务数据并更新参数，无需重新训练。
   该方法可直接迁移至用户留存预测、设备能耗预测等线性关联场景。如需完整代码、数据及更多业务案例，可加入交流社群，与600+行业人士共同探讨贝叶斯方法的实际应用。