当前位置：首页 > news >正文

梯度下降算法

news 2025/9/17 18:24:32

Gradient Descent 梯度下降

一、核心思想：一个最经典的比喻

想象一下，你是一个蒙着眼睛的登山者，被困在一片漆黑的山林中。你的目标是走到山谷的最低点（寻找最低点）。

你会怎么做？

你会用脚感受一下周围的地面，找出哪个方向是“下坡”最陡的。
然后朝着那个最陡的下坡方向迈出一步。
到达新位置后，再次用脚感受，寻找新的最陡下坡方向，再迈出一步。
...如此反复...

直到你感觉到四周都是上坡，无论往哪个方向走，地面都会变高，说明你已经到达了谷底！

这个“感受坡度”和“向下走”的过程，就是梯度下降算法的精髓。

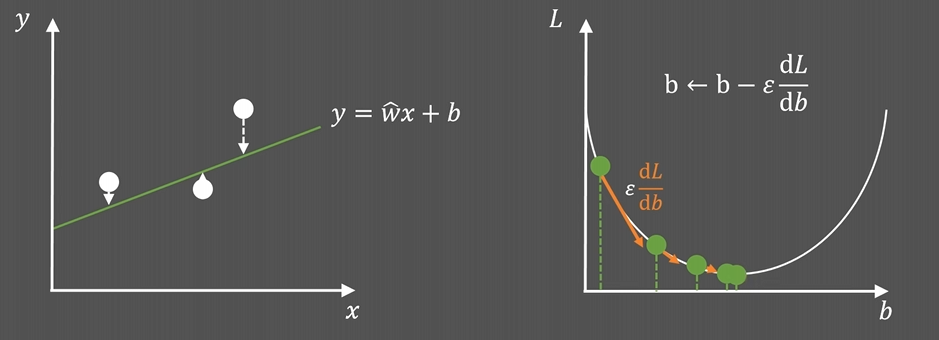
二、把比喻变成数学概念

现在，我们把上面的比喻翻译成机器学习的语言：

比喻	机器学习中的术语
登山者所在的位置	模型当前的参数值 (例如，线性回归中的权重 `w` 和偏差 `b`)
山谷的地形	损失函数 (Loss Function) `J(w, b)`
地面的坡度	梯度 (Gradient) `∇J(w, b)`
最陡的下坡方向	负梯度的方向 `-∇J(w, b)`
迈出一步的步长	学习率 (Learning Rate) `α`
走到谷底	找到使损失函数最小的最优参数 `w, b`

损失函数：一个衡量模型预测值 ŷ 与真实值 y 之间差距的函数。我们的目标就是找到一组参数，让这个损失函数的值最小。常见的损失函数有均方误差（MSE）、交叉熵（Cross-Entropy）等。

梯度：一个向量（矢量），表示函数在某一点处各个方向上的斜率（即变化率最快的方向）。梯度指向函数值增长最快的方向。

三、梯度下降的算法步骤

算法流程可以概括为以下几步，这个过程会循环往复，直到满足停止条件（比如达到最大迭代次数或梯度变得非常小）：

初始化：随机初始化参数 w 和 b。（相当于把登山者随机放在山上的某个点）。
计算梯度：计算当前参数点处的损失函数梯度。
$\text{梯度} = \nabla J(w, b) = \left[ \frac{\partial J}{\partial w}, \frac{\partial J}{\partial b} \right]$
（这相当于用脚感受周围哪个方向最陡）。
更新参数：沿着负梯度（即下坡方向）更新参数。
$w = w - \alpha \cdot \frac{\partial J}{\partial w}$
$b = b - \alpha \cdot \frac{\partial J}{\partial b}$
（这相当于朝着最陡的下坡方向迈出一步）。
重复：重复步骤2和3，直到梯度接近零（无法再下降）或达到预设的迭代次数。
（不断感受、迈步，直到走到谷底）。

四、关键超参数：学习率

学习率是梯度下降中最重要的超参数。

学习率太小：每次迈出的步长非常小。收敛速度慢，需要很多很多步才能到达谷底。
学习率太大：步长太大，一步迈得太远，可能会直接跨过最低点，甚至导致损失函数震荡甚至发散，永远找不到最低点。
学习率设置得当：能以较快的速度稳定地收敛到最小值。

选择合适的学习率需要经验和技巧，有时也会使用自适应学习率的优化算法（如Adam），它们能自动调整学习率的大小。

五、三种常见的梯度下降

根据每次更新参数时使用的数据量不同，分为三种：

批量梯度下降：
- 做法：每次计算梯度和更新参数时，都使用全部的训练数据。
- 优点：梯度方向准确，容易收敛到全局最优。
- 缺点：非常慢，尤其是数据集很大时。
随机梯度下降：
- 做法：每次只随机使用一个训练样本（抽取部分数据）来计算梯度并更新参数。
- 优点：速度快，可以在线学习。
- 缺点：梯度方向波动很大，损失函数会剧烈震荡，不容易收敛到最优点。
小批量梯度下降：
- 做法：每次使用一小批数据（比如32, 64, 128个样本）来计算梯度和更新参数。
- 优点：这是最常用的方法！它平衡了批量梯度下降的稳定性和随机梯度下降的速度，更加高效和稳定。
- 缺点：需要手动设置批量大小（batch size）这个超参数。

总结

梯度下降是一种通过迭代来寻找函数最小值的优化算法。
它的核心是沿着负梯度（最陡下降方向）更新参数。
学习率控制着每一步的步长，至关重要。
小批量梯度下降是实践中最常用的版本。

它就是机器学习和深度学习模型能够“学习”和“自我优化”的根本动力来源。几乎所有神经网络的训练都离不开它（或其变种，如Adam）的驱动。

一、 Adam 是什么？为什么需要它？

Adam 的全称是 Adaptive Moment Estimation（自适应矩估计）。这个名字完美概括了它的核心思想。

在它之前，我们已经有了很多优化器，但它们各有缺点：

SGD（随机梯度下降）：简单但震荡严重，收敛慢。
SGD with Momentum：加入了“动量”，加速收敛，减轻震荡，但对所有参数使用相同的学习率。
Adagrad, RMSprop：自适应地为每个参数调整学习率（对于频繁更新的参数，给予较小的学习率；对于不频繁更新的参数，给予较大的学习率），但它们缺少“动量”概念。

Adam 的诞生就是为了集百家之长：

Adam = Momentum (动量) + RMSprop (自适应学习率) + 偏差校正

它同时考虑了一阶动量（梯度均值，控制方向）和二阶动量（梯度平方的均值，控制步长），并为每个参数自适应地调整学习率。

二、 Adam 的核心思想：两大动量

Adam维护两个状态变量来为每个参数进行自适应调整：

1. 一阶动量（First Moment） - `m_t`

它是什么：梯度的指数移动平均值。它估计了梯度方向的均值。
作用：类似于动量。它积累了过去的梯度方向，使得参数更新方向更加稳定，减少震荡，从而加速在稳定方向的收敛。
物理意义：就像是“速度”。它让优化过程具有“惯性”，不容易被临时的、嘈杂的梯度所带偏。

2. 二阶动量（Second Moment） - `v_t`

它是什么：梯度平方的指数移动平均值。它估计了梯度大小的均值。
作用：类似于 RMSprop。它衡量了历史梯度的大小。对于梯度通常很大的参数，v_t 会很大，从而减小其有效学习率；对于梯度通常很小的参数，v_t 会很小，从而增大其有效学习率。
物理意义：就像是“加速度”。它感知地形变化，在陡峭（梯度大）的地方刹车（小步走），在平坦（梯度小）的地方加速（大步走）。

Adam的巧妙之处在于，它为每个参数都独立地计算和维护这两个动量！

三、 Adam 的算法流程（一步一步详解）

以下是Adam更新参数 θ_t 的完整步骤：

初始化：

m_0 = 0 (一阶动量初始化为0)
v_0 = 0 (二阶动量初始化为0)
t = 0 (时间步初始化为0)

循环（对于每一个时间步 t）：

计算当前梯度：
$g_t = \nabla_\theta J_t(\theta_{t-1})$
- 在时间步 t，计算损失函数关于参数 θ 的梯度 g_t。
更新一阶动量（有偏估计）：
$m_t = \beta_1 \cdot m_{t-1} + (1 - \beta_1) \cdot g_t$
- 用超参数 β1（通常设为0.9）来控制历史动量和当前梯度的权重。这相当于一个指数衰减的平均值。
更新二阶动量（有偏估计）：
$v_t = \beta_2 \cdot v_{t-1} + (1 - \beta_2) \cdot g_t^2$
- 用超参数 β2（通常设为0.999）来控制历史动量和当前梯度平方的权重。
计算一阶动量的偏差校正：
$\hat{m}_t = \frac{m_t}{1 - \beta_1^t}$
- 由于 m0 和 v0 初始化为0，在训练初期（t很小的时候），它们会被“偏向”于0。偏差校正可以消除这种初始化带来的偏差，让估计在训练初期更加准确。
计算二阶动量的偏差校正：
$\hat{v}_t = \frac{v_t}{1 - \beta_2^t}$
更新参数：
$\theta_t = \theta_{t-1} - \alpha \cdot \frac{\hat{m}_t}{\sqrt{\hat{v}_t} + \epsilon}$
- α：全局学习率，需要手动设置。
- ε：一个极小值（通常1e-8），防止分母为零。
- 这一步是Adam的灵魂：
  - \hat{m}_t 提供了稳定的更新方向（动量）。
  - \sqrt{\hat{v}_t} 提供了自适应的学习率。对于梯度大的参数，v_t大，分母大，有效步长 α / √v_t 就小；反之亦然。

为了更直观地展示这个流程，你可以参考以下流程图：

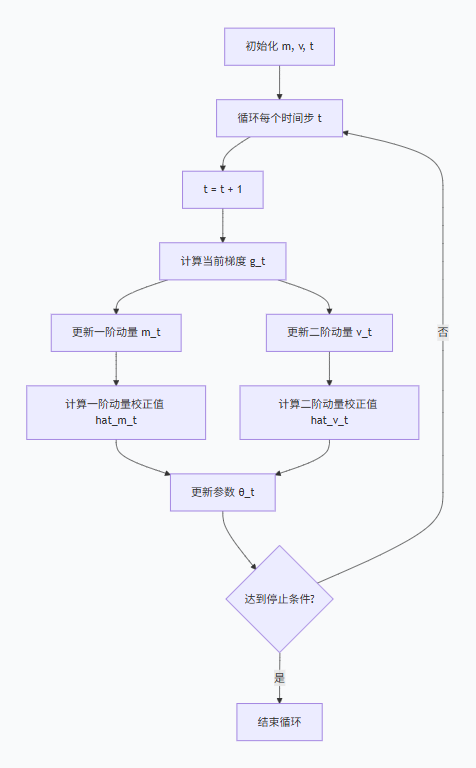
四、 Adam 的超参数

Adam的超参数通常不需要大量调优，因为它们有很强的鲁棒性。

α (学习率)：最重要的超参数。有时需要根据任务进行调整。默认值可以是 0.001 或 3e-4。
β₁：一阶动量的衰减率。控制历史梯度的权重。默认值 0.9。
β₂：二阶动量的衰减率。控制历史梯度平方的权重。默认值 0.999。
ε：数值稳定项。几乎不需要改变，默认 1e-8。

五、为什么 Adam 如此强大和流行？

结合了双重优点：同时拥有了动量的加速收敛能力和自适应学习率的稳定性。
对每个参数的自适应：为每个参数计算不同的学习率，这使得它非常适合处理稀疏梯度的问题（如自然语言处理中的嵌入层）。
实现简单，收敛快：通常默认参数就能取得很好的效果，使得它成为许多研究者和工程师的“首选”优化器。
偏差校正：确保了训练初期的稳定性。

总结

特性	解释
名字	Adaptive Moment Estimation
核心	同时维护一阶动量（方向）和二阶动量（步长）
更新规则	$\theta_t = \theta_{t-1} - \alpha \cdot \frac{\hat{m}_t}{\sqrt{\hat{v}_t} + \epsilon}$
优点	收敛快、效果好、对稀疏数据友好、超参数鲁棒
超参数	`α` (学习率), `β₁` (0.9), `β₂` (0.999), `ε` (1e-8)