RC-Explainer | Reinforced Causal Explainer for Graph Neural Networks

论文信息

论文标题：Reinforced Causal Explainer for Graph Neural Networks
论文作者：Xiang Wang, Yingxin Wu, An Zhang, Fuli Feng, Xiangnan He, Tat-Seng Chua
论文来源：
论文地址：link
论文代码：link

Abstract

​  1. 研究核心背景：GNN 可解释性的重要性与现有方法缺陷​

• • 核心需求：可解释性是探究图神经网络（GNNs）的关键，需回答 “GNN 为何做出某一预测” 的问题。​

• • 主流技术：特征归因（Feature Attribution）是主流解释技术，通过突出输入图中的 “解释性子图”，揭示该子图如何推动 GNN 产生预测结果。​

• • 现有方法路径：现有归因方法多通过梯度类（gradient-like）或注意力分数（attention scores）为边分配重要性，再选择分数 Top 的边构成解释性子图，具体包括：​

• • • 基于梯度信号：通过将模型预测结果反向传播到图结构，获取边的梯度相关重要性；​

• • • 基于掩码 / 注意力：通过掩码函数或注意力网络生成边的掩码 / 注意力分数，用部分图（掩码 / 注意力筛选后）逼近原预测；​

• • • 基于扰动：通过扰动图结构（如移除子图、计算 Shapley 值）观察预测变化，确定边的重要性。​

• • 关键缺陷：现有方法存在一个不合理假设 ——所选边线性独立，完全忽略边之间的依赖关系，尤其是边的 “协同效应”（coalition effect），导致解释性子图存在两大问题：​

1. 1. 1. 不可靠（unfaithful）：无法真实反映 GNN 的决策逻辑，可能包含与预测无关的虚假关联边；
      2. 冗余（verbose）：包含重复或对预测贡献微弱的边，解释效率低；

  2. 提出方法：Reinforced Causal Explainer（RC-Explainer）​

• • 方法定位：基于强化学习（RL）的智能体，专门解决现有方法忽略边依赖与协同效应的问题。​

• • 核心框架：序列决策过程：将解释子图的构建转化为 “逐步添加边” 的序列决策 —— 从空集开始，每次向已选子图中添加 1 条具有显著重要性的边，最终生成完整解释性子图。​

• • 技术细节：​

1. 1. 1. 策略网络（Policy Network）：负责预测 “添加边” 的动作，即判断当前应选择哪条边加入子图；​

      2. 奖励机制（Reward）：量化所选边对 GNN 预测的因果效应（causal effect），核心作用是：​

         1. 考虑新添加边与已选边的依赖关系，判断二者是否能协同形成 “边联盟”（coalition）；​

         2. 若协同效应强（对预测推动作用显著）则给予高奖励，反之则低奖励，避免冗余 / 无关边；​

      3. 训练目标：通过策略梯度（policy gradient）优化边序列的奖励总和，确保生成的解释性子图既可靠又简洁。​

  3. 方法优势与实验结果​

• • 核心优势：​

1. 1. 1. 解释质量：生成的解释性子图更可靠（faithful）、更简洁（concise），能真实反映 GNN 决策逻辑；​

      2. 泛化能力：对未见过的图（unseen graphs）具有更好的泛化性，可适配不同类型的 GNN 模型。​

• • 实验验证：​

• • • 实验场景：在 3 个图分类数据集上，对不同 GNN 模型进行解释；​

• • • 评估维度：​

• • • • 定量指标：预测准确率（Predictive Accuracy，衡量子图还原 GNN 预测的能力）、对比度（Contrastivity，衡量类间解释的区分度）；​

• • • • 定性验证：通过合理性检验（sanity checks）和可视化检查（visual inspections）；​

• • • 结果结论：RC-Explainer 在定量指标上达到或超越当前最先进方法（state-of-the-art），且顺利通过定性验证。​

  4. 补充信息​

• • 代码与数据可获取性：相关代码和数据集已开源，地址为 https://github.com/xiangwang1223/reinforced causal explainer。​

• • 关键词关联：紧密围绕图神经网络（GNNs）、特征归因（Feature Attribution）、可解释方法（Explainable Methods）、因果效应（Cause-Effect）四大核心方向，解决现有技术的因果性与边依赖缺失问题。

1 INTRODUCTION 

1.1 研究背景：GNN 的优势与可解释性需求

  1. GNN 的核心价值

• • 图神经网络（GNNs）在图结构数据相关任务中表现突出，其成功核心在于强大的表示学习能力—— 能以端到端的方式将图的结构信息融入特征表示，适配分子图、社交网络、场景图等各类图数据场景。

  2. 可解释性的必要性

• • 随着 GNN 在公平性、安全性、鲁棒性等关键实际应用（如药物分子毒性预测、社交网络风险识别）中的深入，可解释性成为影响其落地的核心因素。用户需要明确 “GNN 为何做出某一预测”，而非仅依赖黑箱输出。

1.2 研究聚焦的可解释性类型

  本文明确聚焦后验（post-hoc）、局部（local）、模型无关（model-agnostic） 的 GNN 可解释性，三大特性定义如下：

• • 后验（post-hoc）：将待解释的 GNN 视为 “黑箱”，在模型训练完成后，通过额外的解释器分析其预测逻辑，不干预原模型训练过程。

  • 局部（local）：针对单个图实例的预测结果进行解释（如解释某一特定分子为何被判定为致癌），而非对模型整体决策模式做全局分析。

  • 模型无关（model-agnostic）：解释方法不绑定特定 GNN 结构，可适配 GCN、GIN、GAT、APPNP 等各类 GNN 模型，通用性强。

1.3 主流解释范式：特征归因与选择

  1. 范式核心逻辑

• • 特征归因与选择（Feature Attribution and Selection）是当前解释 GNN 的主流范式，核心流程为：

1. 1. 1. 归因分配：将 GNN 的预测结果 “分配” 到输入图的特征（本文聚焦边特征，即结构特征）上，为每条边赋予 “重要性分数”；
      2. 子图构建：筛选重要性分数 Top 的边，组成 “解释性子图”，该子图被认为是推动 GNN 做出目标预测的关键结构。

  2. 现有归因方法的三大技术路径

  现有方法通过不同方式计算边的重要性分数，主要分为三类：

    1.基于梯度类信号（Gradient-like Signals）

• • • 原理：通过将模型预测结果反向传播到图结构，获取边的梯度相关信号（如边权重的梯度），以梯度绝对值衡量重要性；

• • • 代表方法：SA（Sensitivity Analysis）等。

    2.基于掩码 / 注意力分数（Masks/Attention Scores）

• • • 原理：通过掩码函数或注意力网络生成边的掩码值或注意力权重，用 “经过掩码 / 注意力筛选的部分图” 逼近原模型预测，权重越高代表边越重要；

• • • 代表方法：GNNExplainer、PGExplainer、ReFine 等。

    3.基于扰动的预测变化（Prediction Changes on Perturbations）

• • • 原理：通过扰动图结构（如移除子图、修改边存在性），观察模型预测结果的变化，变化越大代表被扰动边越重要；部分方法通过计算 Shapley 值量化这种变化；

• • • 代表方法：PGM-Explainer、SubgraphX、CXPlain 等。

1.4 现有方法的核心缺陷

  本文指出，现有归因方法存在两大未解决的关键问题，导致解释性子图质量不佳：

  1. 无法区分边的因果效应与关联效应

• • 核心问题：现有方法（如梯度类、注意力类）多从 “关联角度” 分析边与预测的关系，无法识别 “因果边”（真正推动预测的边）与 “非因果边”（仅与预测存在虚假关联的边）。

• • 实例佐证（分子图 mutagenicity 预测）：氮 - 碳（N-C）键常与硝基（NO₂）共存，因此与 “致癌” 属性存在虚假关联，SA 等方法会将其列为重要边；但单独输入 N-C 键到 GNN，无法还原 “致癌” 预测，说明该边并非真实因果因素，解释结果不可靠（unfaithful）。

  2. 忽略边之间的依赖关系与协同效应

• • 核心问题：现有方法默认 “边的重要性独立”，未考虑边之间的依赖关系 —— 实际中，边常通过 “协同作用” 形成 “边联盟（coalition）”，共同影响 GNN 预测，单独分析单条边的重要性会遗漏关键协同效应。

• • 实例佐证（分子图 mutagenicity 预测）：

• • • 单独的 N-C 键与 “N-C 键 + 碳 - 碳双键（C=C）” 对预测的提升差异极小（预测致癌概率仅从 0.31 升至 0.35），说明二者无有效协同；

• • • 两条氮 - 氧双键（N=O）可形成硝基（NO₂），这是已知的致癌关键结构，输入两条 N=O 键时，预测致癌概率从 0.72（单条 N=O）升至 0.95，协同效应显著，但现有方法难以捕捉这种联盟作用，导致解释结果冗余（verbose） 或遗漏关键边。

1.5 本文解决方案的核心思路

  为解决上述缺陷，本文提出 “因果筛选策略（Causal Screening Strategy）”，核心逻辑如下：

1. 1. 序列添加边的筛选模式：解释性子图从空集开始，每次仅添加 1 条边，逐步构建，而非一次性筛选 Top-K 边；

   2. 因果效应评估依赖关系：添加边时，基于因果推断（causality）评估 “候选边与已选边的依赖关系”—— 通过对比 “已选边子图 + 候选边”（处理组）与 “仅已选边子图”（控制组）的 GNN 预测差异，计算候选边的 “个体因果效应（ICE）”；

   3. 筛选标准：若 ICE 为正，说明候选边与已选边形成有效联盟，为预测提供独特信息；若为负或接近零，说明候选边冗余或无关，不纳入解释性子图。

  在此基础上，本文进一步设计强化学习（RL）智能体 RC-Explainer，通过策略网络学习 “最优边选择序列”，实现高效的因果筛选，最终生成既可靠又简洁的解释性子图。

1.6 研究贡献

1. 强调边的因果效应与依赖关系对 GNN 解释质量的关键作用，突破现有方法的 “边独立假设”；

2. 将 GNN 解释任务转化为序列决策过程，提出 RL-based 的 RC-Explainer，从因果角度分析边依赖；

3. 在三个数据集上通过定量指标（预测准确率、对比度）、合理性检验、可视化验证，证明 RC-Explainer 的有效性。

2 RELATED WORK

2.1 可解释性方法的核心分类框架​

  本文首先明确可解释性研究领域的三大核心二分法，为后续相关工作梳理提供分类标准，具体如下：

  后验（Post-hoc）vs 内在（Intrinsic）

1. 1. 后验：通过额外的解释器对已训练完成的 “黑箱模型”（如 GNN）进行解释，不改变原模型结构与训练过程

   2. 内在：模型本身具备可解释性（如线性模型、决策树），无需额外解释器

  局部（Local）vs 全局（Global）

1. 1. 局部：针对单个数据实例（如图结构）的预测结果进行解释，回答 “为何该实例被预测为某类”

   2. 全局：对模型整体决策模式进行解释，揭示 “模型通常依据哪些特征做决策”

  模型无关（Model-agnostic）vs 模型特定（Model-specific）

1. 1. 模型无关：解释方法不绑定特定模型结构，可适配 GCN、GIN、APPNP 等各类 GNN

   2. 模型特定：为某类特定模型（如仅针对 GAT）定制解释逻辑，依赖模型内部组件

  本文研究严格聚焦后验、局部、模型无关的可解释性方法，后续相关工作梳理均围绕该方向展开。

2.2 非图神经网络（非 GNN）的可解释性方法​

  非 GNN 场景（如 CNN、普通神经网络）的可解释性研究起步更早，形成了成熟的特征归因技术体系，本文将其归纳为三大类，为 GNN 可解释性方法提供借鉴：​

  1. 基于反向传播的梯度类方法​

• • 核心原理：通过反向传播将模型预测结果映射回输入特征，以 “梯度信号” 量化特征重要性 —— 梯度绝对值越大，代表该特征对预测结果的影响越显著。​

• • 典型方法：​

• • • Gradient：直接使用输入特征对模型输出的偏导数作为重要性分数；​

• • • GradCAM：在梯度基础上结合网络层的上下文信息（如 CNN 的卷积层特征图），提升梯度信号的可靠性，尤其适用于图像分类任务；​

• • • 其他延伸方法：通过对梯度进行归一化、平滑处理，解决梯度消失或噪声干扰问题。​

• • 适用场景：适用于输入特征为连续值（如图像像素）或离散值（如文本词向量）的非图结构数据，计算效率高，但仅能捕捉特征与预测的 “关联关系”，无法区分因果。​

  2. 基于可训练掩码 / 注意力的方法​

• • 核心原理：引入额外的可训练网络（掩码网络或注意力网络），通过优化 “掩码 / 注意力筛选后的特征对模型预测的逼近程度”，学习特征的重要性 —— 掩码值 / 注意力权重越高，特征越重要。​

• • 典型方法：​

• • • L2X（Learning to Explain）：训练特征掩码网络，以 “掩码特征与原模型预测的互信息最大化” 为目标，筛选出对预测最关键的特征子集；​

• • • 注意力网络延伸：在 Transformer 等模型中，直接利用原生注意力权重作为特征重要性，或为非注意力模型额外添加注意力层学习特征权重。​

• • 适用场景：需要稀疏解释结果（如仅保留关键特征）的场景，但需额外训练掩码 / 注意力网络，且可能因网络过拟合导致解释结果失真。​

  3. 基于输入扰动的方法​

• • 核心原理：通过主动扰动输入特征（如遮蔽、移除、修改特征），观察模型预测结果的变化，以 “预测变化幅度” 衡量特征重要性 —— 扰动后预测偏差越大，特征对预测的贡献越关键。​

• • 典型方法：​

• • • CXPlain：通过遮蔽单个特征并计算 “遮蔽前后预测概率的差异”，量化特征的边际效应，同时考虑预测不确定性；​

• • • 其他延伸：通过随机扰动多个特征组合，分析特征间的交互作用，但计算成本较高。​

• • 适用场景：需要验证特征 “必要性” 的场景（如移除特征后预测失效，说明特征是关键），但扰动方式可能破坏数据结构（如文本中移除关键词导致语义断裂），影响结果可靠性。​

2.3 图神经网络（GNN）的可解释性方法​

  GNN 因输入为图结构（含节点、边及拓扑关系），其可解释性方法在借鉴非 GNN 技术的基础上，需适配图的结构特性，本文将其分为三类，同时明确与本文方法的差异：​

  1. 基于图结构梯度类信号的方法​

• • 核心原理：将非 GNN 的梯度方法适配到图结构，通过反向传播计算 “模型输出对图结构特征（边权重、节点特征）的梯度”，以梯度信号衡量边 / 节点的重要性。​

• • 典型方法：​

• • • SA（Sensitivity Analysis）：计算 GNN 损失函数对邻接矩阵（边存在性）的梯度，梯度绝对值作为边的重要性分数；​

• • • GNN-GradCAM：延伸 GradCAM 思想，结合 GNN 各层的节点表示上下文，优化梯度信号，提升边 / 节点重要性评估的准确性。​

• • 局限性：与非 GNN 梯度方法类似，仅捕捉关联关系，易受图中虚假关联边（如与关键边共现但无关的边）干扰，且未考虑边间依赖关系。​

  2. 基于图结构掩码 / 注意力的方法​

• • 核心原理：为 GNN 设计专用的掩码或注意力机制，学习图结构特征（边、节点）的重要性，适配图的拓扑依赖性。​

• • 典型方法：​

• • • GNNExplainer：为每个图实例单独训练边掩码，以 “掩码子图的预测与原图预测的相似度最大化 + 掩码稀疏性最大化” 为目标，筛选关键边；​

• • • PGExplainer（Parameterized Explainer）：训练一个共享的参数化网络，为多个图实例生成边掩码，避免 GNNExplainer “单图单训练” 的低效问题；​

• • • ReFine：先在类别级图数据上预训练注意力网络，学习全局类别相关的重要特征模式，再针对单个图实例微调局部注意力，平衡全局与局部解释。​

• • 局限性：多数方法仍假设 “边的重要性独立”，忽略边间的协同效应（如分子图中硝基的 N=O 键联盟）；且部分方法（如 GNNExplainer）为单图训练掩码，计算成本高，泛化性差。​

  3. 基于图结构扰动的方法​

• • 核心原理：通过扰动图的结构（如移除节点、删除边、修改边连接关系），观察 GNN 预测变化，量化边 / 节点的重要性，部分方法结合概率模型或搜索算法优化扰动效率。​

• • 典型方法：​

• • • PGM-Explainer（Probabilistic Graphical Model Explainer）：对节点进行随机扰动，基于扰动 - 预测数据学习贝叶斯网络，识别对预测有显著影响的节点子集；​

• • • SubgraphX：采用蒙特卡洛树搜索（MCTS）算法探索不同子图组合，结合 Shapley 值量化子图对预测的贡献，筛选最优解释性子图；​

• • • CXPlain（GNN 适配版）：通过遮蔽图中的边，计算遮蔽前后预测概率的差异，评估边的重要性。​

• • 局限性：Shapley 值计算复杂度随图规模指数增长，难以应用于大图；部分扰动方法（如随机移除边）可能破坏图的连通性，导致 GNN 无法正常提取特征，影响预测变化评估的准确性。​

  4. 特殊对比方法：XGNN​

• • 方法特点：聚焦 “模型级（Model-level）” 解释，旨在揭示 GNN 整体决策依赖的 “原型模式”（如某类分子的共同结构），而非针对单个图实例的局部解释；​

• • 与本文差异：XGNN 的解释结果可能不是输入图中真实存在的子结构，无法保证 “局部保真度”（Local Fidelity）；而本文 RC-Explainer 为局部解释，解释子图是输入图的子集，且结合全局模型认知保证保真度。​

2.4 本文方法与相关工作的核心差异​

  本文 RC-Explainer 与现有 GNN 可解释性方法的关键区别在于突破 “边独立假设”：​

1. 1. 现有方法（如 SA、GNNExplainer、PGM-Explainer）多独立评估单条边的重要性，忽略边间依赖与协同效应；​

   2. 本文将解释任务重构为序列决策过程，通过因果效应评估 “候选边与已选边的依赖关系”，明确捕捉边的联盟作用（如硝基的 N=O 键协同），最终生成更可靠、简洁的解释性子图。

3 PRELIMINARIES

3.1 图神经网络（GNN）背景知识

  图数据的形式化定义

• • 单图实例：用 $ \mathcal{G} = \{e \mid e \in \mathcal{E}\} $ 表示，其中一条边 $ e = (v, u) \in \mathcal{E} $ 连接两个节点 $ v, u \in \mathcal{V} $ （ $ \mathcal{V} $ 为节点集合， $ \mathcal{E} $ 为边集合），边的核心作用是突出图的 “结构特征”（即边的存在性及其端点关联）。

• • 节点特征：每个节点 $ v $ 配备 $ d $ - 维特征向量 $ x_v \in \mathbb{R}^d $ ，是 GNN 学习表示的重要输入（本文暂不聚焦节点特征解释，仅关注边的结构特征）。

3.2 GNN 可解释性任务描述

  1. 任务核心目标：回答核心问题：“给定目标图实例 $ \mathcal{G} $ ，是什么因素决定了 GNN 模型 $ f $ 输出预测结果 $ \hat{y}_c $ ？”

    本文采用特征归因（Feature Attribution） 范式实现该目标 —— 这是局部、后验、模型无关可解释性的主流技术。

  2. 任务形式化定义

• • 核心操作：将 GNN 的预测结果 $ \hat{y}_c $ 分解到输入图的结构特征（即边）上，为每条边分配 “重要性分数”，衡量其对预测 $ \hat{y}_c $ 的贡献度。

• • 最终输出：筛选重要性分数 Top-K 的边，构建 “解释性子图” $ \mathcal{G}_K^* = \{e_1^*, \cdots, e_K^*\} \subseteq \mathcal{G} $ ，其中 $ e_k^* $ 为第 $ k $ 重要的边。

    该子图需满足 “忠实性”—— 能为 GNN 的预测 $ \hat{y}_c $ 提供明确支持，即输入 $ \mathcal{G}_K^* $ 到 GNN，应能近似还原原预测 $ \hat{y}_c $ 。

  3. 任务范围限定

    本文明确聚焦结构特征（边的存在性及其端点） 的解释，暂不涉及 “节点内容特征（如节点属性 $ x_v $ ）” 的归因 —— 节点特征的重要性识别被列为未来研究方向，当前仅通过边的筛选构建解释性子图。

4 METHODOLOGY

  

4.1 章节核心目标

　　本章围绕 “生成忠实且简洁的 GNN 解释性子图” 展开，先指出 “整体子图因果归因” 的局限性，再提出 “边序列因果筛选” 策略，最终设计基于强化学习的RC-Explainer实现该策略，核心解决 “边的因果效应识别” 与 “边间依赖关系捕捉” 两大关键问题。

4.2 第一步：整体子图的因果归因（基础框架与局限）

1. 核心思路

  从因果推断视角定义 “子图重要性”，通过优化 “子图对预测的因果贡献” 筛选最优解释性子图。形式化目标为：

     $ \mathcal{G}_K^* = \arg\max_{\mathcal{G}_K \subseteq \mathcal{G}} A(\mathcal{G}_K \mid \hat{y}_c) $

    其中：

• • • $ \mathcal{G}_K $ ：含 K 条边的候选子图（ $ |\mathcal{G}_K|=K $ ）；

• • • $ A(\cdot) $ ：归因函数，量化子图对目标预测 $ \hat{y}_c = f(\mathcal{G}) $ 的因果效应；

  目标：在所有含 K 条边的子图中，选择因果贡献最大的 $ \mathcal{G}_K^* $ 作为解释性子图。

2. 因果归因函数的设计（基于干预与互信息）

  为避免 “关联关系干扰”，引入因果推断中的 do(·)（干预操作） 定义归因函数 $ A(\mathcal{G}_K \mid \hat{y}_c) $ ：

• 干预操作：

• 处理组： $ do(\mathcal{G} = \mathcal{G}_K) $ ，即强制 GNN 输入为候选子图 $ \mathcal{G}_K $ ；

• 控制组： $ do(\mathcal{G} = \emptyset) $ ，即强制 GNN 输入为空图（无信息参考）。

• 个体因果效应（ICE）：通过对比处理组与控制组的 “子图 - 预测互信息” 差异，量化子图的因果贡献，公式如下：

     $ A(\mathcal{G}_K \mid \hat{y}_c) = I(do(\mathcal{G}_K); \hat{y}_c) - I(do(\emptyset); \hat{y}_c) $

    其中

• • • $ I(\cdot; \cdot) $ 为互信息，衡量 “干预后子图” 与 “目标预测 $ \hat{y}_c $ ” 的信息关联度；

    • $ I(do(\mathcal{G}_K); \hat{y}_c) = H(\hat{y}_c) - H(\hat{y}_c \mid do(\mathcal{G}_K)) $ （ $ H(\cdot) $ 为熵， $ H(\hat{y}_c \mid do(\mathcal{G}_K)) $ 为干预后预测的条件熵）。

3. 局限性（为何需改进）

  直接优化上述目标存在两大障碍，无法落地：

• • 计算复杂度高（NP-hard）：候选子图数量随边数呈指数增长（如含 M 条边的图，选 K 条边的组合数为 $ C(M, K) $ ），无法遍历所有可能子图；

• • 缺乏组件级解释：仅能评估子图整体的因果贡献，无法区分子图中 “关键边” 与 “冗余边”，不符合 “局部解释需明确个体特征重要性” 的需求。

4.3 第二步：边序列的因果筛选（核心改进策略）

  为解决整体子图归因的局限，提出因果筛选策略—— 将 “一次性选 K 条边” 转化为 “逐步添加边” 的序列过程，动态评估每条边的因果效应及与已选边的依赖关系。

1. 策略核心逻辑

• 初始状态：解释性子图从空集 $ \mathcal{G}_0^* = \emptyset $ 开始；

• 序列选择：第 k 步（ $ k=1,2,\cdots,K $ ）从剩余边候选池 $ \mathcal{O}_k = \mathcal{G} \setminus \mathcal{G}_{k-1}^* $ 中，选择 1 条边 $ e_k^* $ 加入子图，更新为 $ \mathcal{G}_k^* = \mathcal{G}_{k-1}^* \cup \{e_k^*\} $ ；

• 选择准则：第 k 步的最优边 $ e_k^* $ 需最大化 “给定已选子图 $ \mathcal{G}_{k-1}^* $ 时，边 $ e_k $ 对预测的因果效应”，形式化目标为：

     $ e_k^* = \arg\max_{e_k \in \mathcal{O}_k} A(e_k \mid \mathcal{G}_{k-1}^*, \hat{y}_c) $

2. 边级因果效应的计算（关键改进）

  归因函数 $ A(e_k \mid \mathcal{G}_{k-1}^*, \hat{y}_c) $ 专门评估 “候选边与已选边的依赖关系”，通过干预对比实现：

• 干预操作：

• 处理组： $ do(\mathcal{G} = \mathcal{G}_{k-1}^* \cup \{e_k\}) $ ，输入 “已选子图 + 候选边”；

• 控制组： $ do(\mathcal{G} = \mathcal{G}_{k-1}^*) $ ，输入 “仅已选子图”。

• 因果效应公式：

     $ A(e_k \mid \mathcal{G}_{k-1}^*, \hat{y}_c) = I(do(\mathcal{G}_{k-1}^* \cup \{e_k\}); \hat{y}_c) - I(do(\mathcal{G}_{k-1}^*); \hat{y}_c) $

    进一步化简为条件熵差异（结合图分类任务的概率特性）：

     $ A(e_k \mid \mathcal{G}_{k-1}^*, \hat{y}_c) = -p_{\theta}(\hat{y}_c \mid \mathcal{G}) \log \frac{p_{\theta}(\hat{y}_c \mid \mathcal{G}_{k-1}^*)}{p_{\theta}(\hat{y}_c \mid \mathcal{G}_{k-1}^* \cup \{e_k\})} $

    其中

• • • 符号含义： $ p_{\theta}(\hat{y}_c \mid \cdot) $ 为 GNN 对目标类别 $ \hat{y}_c $ 的预测概率；

    结果解读：若值为正，说明候选边与已选边形成 “有效联盟”，为预测提供独特信息；若为负 / 接近零，说明候选边冗余或无关。

3. 贪心穷举搜索的局限（为何引入 RL）

  直接通过 “贪心穷举” 实现因果筛选（计算所有候选边的 A 值，选最大者）存在缺陷：

• • 缺乏全局认知：逐图单独解释，无法学习不同图间的共性模式（如类别级关键边联盟），泛化性差；

• • 计算效率低：每步需遍历所有候选边，大图场景（如社交网络）中候选边数量多，时间复杂度为 $ O(2(|\mathcal{G}|-K) \times K/2) $ ，难以落地。

4.4 第三步：RC-Explainer 设计（强化学习实现因果筛选）

  为解决贪心搜索的局限，将 “边序列因果筛选” 建模为马尔可夫决策过程（MDP），设计强化学习智能体 RC-Explainer，通过策略网络学习 “全局最优边选择策略”。

1. MDP 建模：四大核心组件

• 状态（State）：第 k 步状态 $ s_k = \mathcal{G}_k $ （已选边构成的子图），初始状态 $ s_0 = \emptyset $

• 动作（Action）：第 k 步动作 $ a_k = e_k $ （从候选池 $ \mathcal{O}_k = \mathcal{G} \setminus \mathcal{G}_{k-1} $ 选 1 条边加入子图）

• 状态转移：执行动作 $ a_k = e_k $ 后，状态从 $ s_{k-1} = \mathcal{G}_{k-1} $ 转移为 $ s_k = \mathcal{G}_{k-1} \cup \{e_k\} $

• 奖励（Reward）：量化动作质量，结合 “边的因果效应” 与 “子图预测有效性”，公式见下文

  奖励函数设计（核心引导信号）

  奖励 $ R(\mathcal{G}_{k-1}, e_k) $ 同时保证 “边的因果有效性” 与 “子图的预测忠实性”：

     $ R(\mathcal{G}_{k-1}, e_k) = \begin{cases} A(e_k \mid \mathcal{G}_{k-1}, \hat{y}_c) + 1, & \text{若 } f_{\theta}(\mathcal{G}_{k-1} \cup \{e_k\}) = \hat{y}_c \\ A(e_k \mid \mathcal{G}_{k-1}, \hat{y}_c) - 1, & \text{否则} \end{cases} $

• 正向奖励：若候选边的因果效应为正（有效），且加入后子图仍能正确预测 $ \hat{y}_c $ ，额外加 1；

• 负向惩罚：若加入候选边后子图预测错误，额外减 1，避免选择 “破坏预测” 的边。

2. 策略网络（Policy Network）：学习边选择概率

  策略网络 $ q_{\phi} $ （参数为 $ \phi $ ）的核心是 “给定当前状态 $ \mathcal{G}_{k-1} $ 与目标预测 $ \hat{y}_c $ ，输出候选边的选择概率”，分两步实现：

  Step1：动作候选表示学习（边的特征编码）

  为每条候选边 $ e_k = (v, u) $ 生成表示向量，捕捉边的结构与特征信息：

     $ z_{e_k} = MLP_1([z_v \parallel z_u \parallel x_{e_k}]) $

• 组件说明：

• $ z_v, z_u $ ：边端点 $ v, u $ 的节点表示，由另一个训练的 GNN 模型 $ g_{\mu} $ （参数 $ \mu $ 可训练）生成；

• $ x_{e_k} $ ：边的预定义特征（无特征时可忽略）；

• $ \parallel $ ：向量拼接操作；

• $ MLP_1 $ ：单隐藏层 MLP（激活函数为 ReLU），输出边表示 $ z_{e_k} \in \mathbb{R}^{d''} $ 。

  Step2：动作选择概率计算（类特异性评分）

  结合 “边表示” 与 “当前子图表示”，计算每条候选边的选择重要性，再通过 Softmax 转化为概率：

  ① 子图表示：当前子图 $ \mathcal{G}_{k-1} $ 的表示 $ z_{\mathcal{G}_{k-1}} $ ，由 GNN $ g_{\mu} $ 对 $ \mathcal{G}_{k-1} $ 做图级读出得到；

  ② 重要性评分：用类特异性 MLP（对应目标类别 $ \hat{y}_c $ ）计算边的重要性：

     $ p_{e_k} = MLP_{2,c}([z_{e_k} \parallel z_{\mathcal{G}_{k-1}}]) $

  ③ 概率分布：对所有候选边的 $ p_{e_k} $ 做 Softmax，得到选择概率：

     $ P_{\phi}(e_k \mid \mathcal{G}_{k-1}, \hat{y}_c) = Softmax_{\mathcal{A}_k}(p_{e_k}) $

 

  其中 $ \mathcal{A}_k $ 为第 k 步候选边集合，类特异性 MLP 确保网络学习 “类别相关的边选择模式”（如致癌分子中优先选 N=O 键）。

3. 策略梯度训练（优化策略网络）

  因边选择是离散动作，无法直接用 SGD 优化，采用REINFORCE 算法（策略梯度方法）最大化 “奖励期望”，训练目标为：

     $ \max_{\phi} \mathbb{E}_{\mathcal{G} \in \mathcal{O}} \mathbb{E}_k \left[ R(\mathcal{G}_{k-1}, e_k) \log P_{\phi}(e_k \mid \mathcal{G}_{k-1}, \hat{y}_c) \right] $

• 优化逻辑：通过梯度上升，增加 “高奖励动作” 的选择概率 —— 即让网络更倾向于选择 “因果效应强、能维持子图预测正确” 的边，最终学习到全局最优的边选择序列。

4.5 关键讨论：时间复杂度与潜在局限

1. 时间复杂度分析

  解释单图 $ \mathcal{G} $ 的时间主要来自两部分：

• • 节点表示学习：GNN $ g_{\mu} $ 生成节点表示的复杂度为 $ O(\sum_{l=1}^L |\mathcal{G}| \times d_l \times d_{l-1}) $ （ $ d_l $ 为第 l 层表示维度）；

• • 边选择过程：第 k 步生成候选边表示的复杂度为 $ O(|\mathcal{A}_k| \times 2d' \times d'') $ ，预测动作的复杂度为 $ O(|\mathcal{A}_k| \times d'') $ ，总复杂度为 $ O(\sum_{k=1}^K |\mathcal{A}_k| \times (2d' \times d'' + d'')) $ ；

  整体结论：中小规模图上效率优于 GNNExplainer、PGM-Explainer，但大规模图因候选边多（动作空间大），效率仍需优化。

2. 潜在局限

• 大规模图效率问题：动作空间随边数增长，导致边选择概率计算耗时，需后续优化动作空间剪枝；

• OOD（分布外）问题：干预生成的子图（如仅含少量边）可能偏离原数据分布（如不符合原图的度分布、连通性），导致因果效应评估失真，需结合反事实生成解决。

4.6 本章核心价值

• 方法创新：首次将 “因果筛选” 与 “强化学习” 结合，突破 “边独立假设”，同时捕捉边的因果效应与依赖关系；

• 落地性：通过策略网络学习全局模式，既保证解释的忠实性（因果效应引导），又提升泛化性（适配 unseen 图）与效率（避免穷举），为后续实验验证奠定方法基础。

5 EXPERIMENTS​

5.1 实验基础：数据集介绍​

  实验采用 3 个主流图分类数据集，覆盖分子图、社交网络、场景图三大典型场景，分别训练不同 GNN 作为待解释模型，数据集详情与模型配置如下表所示：​

维度	Mutagenicity（分子图）	REDDIT-MULTI-5K（社交网络）	Visual Genome（场景图）
图数量	4,337	4,999	4,443
类别数量	2（致癌 / 非致癌）	5（不同问答社区主题）	5（体育馆、街道、农场、冲浪、森林）
平均节点数	30.32	508.52	35.32
平均边数	30.77	594.87	18.04
数据划分比例	训练集：验证集：测试集 = 80%:10%:10%	训练集：验证集：测试集 = 80%:10%:10%	训练集：验证集：测试集 = 80%:10%:10%
数据特点	边对应分子中原子间化学键，标签基于分子对细菌的致癌性	边对应用户间交互关系，标签为社区讨论主题	边对应图像中物体间关系，节点含图像区域特征

5.2 对比基线方法（Baselines）介绍​

  实验选取 6 种主流 GNN 可解释性方法作为基线，覆盖梯度类、掩码类、注意力类、扰动类四大类型，具体如下：​

方法类型	方法名称	核心原理	适配场景与特点
梯度类	SA（Sensitivity Analysis）	通过反向传播计算 GNN 损失函数对邻接矩阵（边存在性）的梯度，以梯度绝对值作为边重要性分数	计算速度快，无需额外训练，但易受梯度噪声干扰，无法区分因果与关联关系
梯度类	Grad-CAM（GNN 适配版）	结合 GNN 各层节点表示的上下文信息优化梯度信号，提升边 / 节点重要性评估的可靠性	比 SA 更稳定，可捕捉局部结构上下文，在含节点特征的场景（如 Visual Genome）表现较好
掩码类	GNNExplainer	为每个图实例单独训练边掩码，以 “掩码子图预测与原图预测相似度最大化 + 掩码稀疏性最大化” 为目标筛选关键边	可生成稀疏解释性子图，但需为单图单独训练，计算成本高，泛化性差
注意力类	PGExplainer（Parameterized Explainer）	训练共享参数化网络为多个图生成边掩码，避免 GNNExplainer “单图单训” 的低效问题	比 GNNExplainer 泛化性更强，可学习类别级边选择模式，但仍忽略边间协同效应
扰动类	CXPlain（GNN 适配版）	通过遮蔽单条边并计算 “遮蔽前后预测概率差异”，量化边的边际效应，考虑预测不确定性	基于扰动验证边的必要性，可捕捉部分因果关系，但扰动可能破坏图连通性影响结果
扰动类	PGM-Explainer（Probabilistic Graphical Model Explainer）	对节点进行随机扰动，基于扰动 - 预测数据学习贝叶斯网络，识别对预测有显著影响的节点 / 边	可建模特征间依赖关系，但 Shapley 值计算复杂度高，大图场景难以应用

5.3 实验内容与对应结论​

  实验围绕 “RC-Explainer 是否能生成更合理的 GNN 解释” 展开，从定量指标（预测准确率、对比度、合理性检验）、时间复杂度、可视化验证三个维度设计实验，具体内容与结论如下：​

5.3.1 实验一：预测准确率评估（衡量解释子图的忠实性）​  

  

  

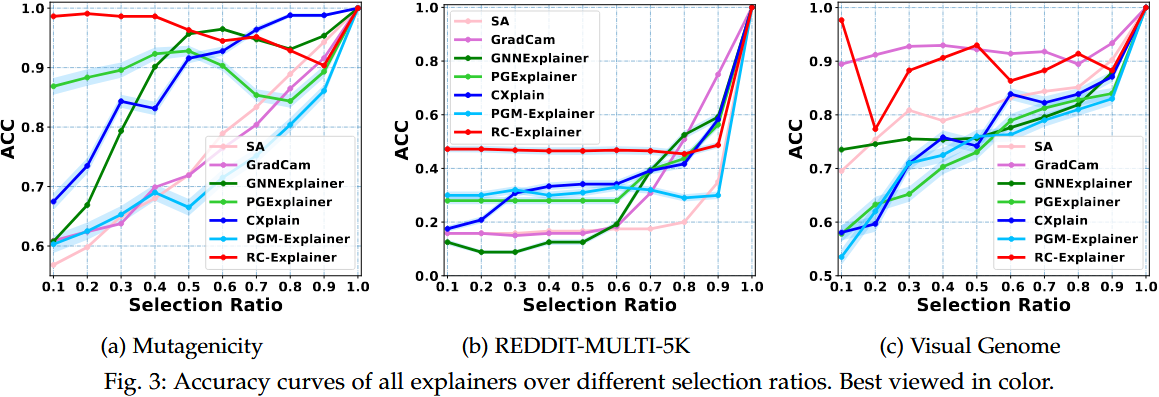
  实验内容​

• • 核心指标：​

• • • ACC@K：选择占原图 10%（K=⌈10%×|G|⌉）的边构成解释性子图，输入 GNN 后还原原预测的准确率，衡量子图对预测的支撑能力；​

• • • ACC-AUC：绘制不同选择比例（0.1~1.0）下的 ACC 曲线，计算曲线下面积，综合评估子图在不同稀疏度下的忠实性。​

• • 实验操作：在 3 个数据集上分别计算 RC-Explainer 与 6 种基线的 ACC@10% 和 ACC-AUC，重复 5 次取平均值。​

  实验结论​

• • RC-Explainer 在 3 个数据集上表现最优：​

• • • Mutagenicity 的 ACC@10% 达 98.6%，远超次优基线 CXPlain（86.8%），ACC-AUC 为 0.964（接近最优保真度）；​

• • • REDDIT-MULTI-5K 的 ACC@10% 达 47.2%，比次优基线 PGM-Explainer（30.0%）提升 25.51%；​

• • • Visual Genome 的 ACC@10% 达 97.6%，与最优基线 Grad-CAM（89.4%）相比仍显著领先，仅 ACC-AUC（0.901）略低于 Grad-CAM（0.917）。​

• • 关键原因：RC-Explainer 的 “因果筛选” 能区分因果边与虚假关联边，同时捕捉边的协同效应（如分子图中硝基的 N=O 键联盟），减少冗余边，提升子图忠实性。​

5.3.2 实验二：对比度评估（衡量解释的类间区分度）​  

  

  实验内容​

• • 核心指标：对比度（CST），通过计算 “目标类别与其他类别（标签置换后）的边重要性排名的斯皮尔曼相关系数绝对值” 衡量解释的类间差异 ——CST 值越低，说明类间解释区分度越高。​

• • 实验操作：对每个图实例，置换其预测标签为其他类别，计算 RC-Explainer 与基线在不同类别下的边重要性排名相关性，取平均值作为 CST。​

  实验结论​

• • RC-Explainer 的解释具有优秀的类间区分度：​

• • • Visual Genome 中 CST 最低（0.306），说明其能为 “街道”“森林” 等不同场景生成差异显著的解释（如 “街道” 优先选 “车 - 在 - 路” 边，“森林” 优先选 “树 - 在 - 地面” 边）；​

• • • Mutagenicity 中 CST 排名第二（0.311），仅略高于 PGExplainer（0.202），可有效区分 “致癌” 与 “非致癌” 分子的关键边（致癌分子选 N=O 键，非致癌分子选 C-H 键）；​

• • • REDDIT-MULTI-5K 中 CST 排名第四（0.481），因大图中随机添加的冗余边轻微提升了类间排名相关性，但仍优于 SA、Grad-CAM 等基线。

  对比度（Contrastivity, CST）：衡量解释的类间区分度

    1. 核心定义与设计初衷​

• • • 定义：对比度是评估 GNN 解释方法 “类间解释区分能力” 的定量指标，核心逻辑是：合理的解释应随目标预测类别的变化而显著变化—— 即对同一图实例，若预测类别从 A 变为 B，解释性子图的关键边应完全不同，而非重复或高度相似。​

• • • 设计初衷：解决现有解释方法 “类间解释同质化” 问题（如部分梯度类方法对不同类别预测输出相似的重要边排名），确保解释能反映模型对不同类别的决策边界差异，符合人类对 “不同类别需不同依据” 的认知逻辑。

    2. 计算原理与公式

• • • 核心思路：通过 “标签置换” 构建 “类间对比场景”，再用斯皮尔曼等级相关系数（Spearman's Rank Correlation） 量化 “原类别解释” 与 “置换类别解释” 的相似性 —— 相似性越低，对比度越好（CST 值越小）。
    • 具体步骤

1. 1. 1. 1. 确定目标与对比类别：对任意图实例 $ \mathcal{G} $ ，设其原预测类别为 $ \hat{y}_c $ ，从其他类别中随机选择一个置换类别 $ s $ （ $ s \neq \hat{y}_c $ ）；

         2. 生成两类解释的边重要性排名：用解释方法分别为 $ \hat{y}_c $ 和 $ s $ 生成所有边的重要性分数，再对两条边分数序列按从高到低排序，得到两个 “边重要性排名列表” $ \Phi(\mathcal{G}, \hat{y}_c) $ （原类别）和 $ \Phi(\mathcal{G}, s) $ （置换类别）；

         3. 计算等级相关系数：计算 $ \Phi(\mathcal{G}, \hat{y}_c) $ 与 $ \Phi(\mathcal{G}, s) $ 的斯皮尔曼等级相关系数 $ \rho $ ，取其绝对值 $ |\rho| $ ；

         4. 求期望得到 CST：对所有图实例、所有可能的置换类别 $ s $ 求平均，得到最终的对比度分数：

         5. $ CST = \mathbb{E}_{\mathcal{G} \sim \mathbb{G}} \mathbb{E}_{s \neq \hat{y}}[|\rho(\Phi(\mathcal{G}, s), \Phi(\mathcal{G}, \hat{y}_c))|] $

• • • 符号说明： $ \mathbb{G} $ 为图实例集合， $ \Phi(\mathcal{G}, \cdot) $ 为解释方法输出的边重要性分数序列， $ |\rho(\cdot)| $ 为斯皮尔曼等级相关系数的绝对值（范围：0~1）。

    3. 结果解读标准

• • • CST 值越低越好：

• • • 若 $ CST \approx 0 $ ：说明 “原类别解释” 与 “置换类别解释” 的边重要性排名几乎无关，解释具备极强的类间区分度（如为 “街道” 场景选 “车 - 在 - 路” 边，为 “森林” 场景选 “树 - 在 - 地面” 边）；

• • • 若 $ CST \approx 1 $ ：说明两类解释的边排名高度相似，解释不具备类间区分能力（如无论预测为 “致癌” 还是 “非致癌”，均优先选择 C-H 键），无法反映模型的类间决策差异。

5.3.3 实验三：合理性检验（验证解释的模型依赖性）​

  实验内容​

• • 核心指标：合理性检验分数（SC），对比 “训练完成的 GNN” 与 “参数随机初始化的未训练 GNN” 的边重要性排名相关性 ——SC 值越低，说明解释依赖 GNN 的真实决策逻辑，而非随机特征，通过检验。​

• • 实验操作：分别为训练 GNN 和未训练 GNN 生成解释，计算边重要性排名的斯皮尔曼相关系数绝对值，取平均值作为 SC。​

  实验结论​

• • RC-Explainer 安全通过合理性检验：​

• • • Mutagenicity 的 SC 为 0.248（排名第三），远低于 PGM-Explainer（0.597），说明其解释不依赖随机特征，能反映 GNN 的真实决策；​

• • • Visual Genome 的 SC 为 0.309（排名第二），仅高于 CXPlain（0.266），验证了解释与 GNN 模型的强关联性；​

• • • REDDIT-MULTI-5K 的 SC 为 0.465（排名第四），虽高于部分基线，但仍低于 Grad-CAM（0.537）、CXPlain（0.696），说明其解释具备模型依赖性。  

  合理性检验分数（Sanity Check Score, SC）：验证解释的模型依赖性

  1. 核心定义与设计初衷

• • 定义：合理性检验分数是评估 GNN 解释方法 “是否依赖目标模型真实决策逻辑” 的定量指标，核心逻辑是：可靠的解释应仅对 “训练完成的 GNN” 有效，对 “随机初始化的未训练 GNN” 无效—— 即解释是基于模型学到的规律，而非输入图的随机特征（如边的高频出现但无关预测）。

• • 设计初衷：揭露 “伪解释”（如部分方法的解释仅与图的固有结构相关，与模型决策无关），确保解释能真实反映目标 GNN 的内部工作机制，而非无意义的随机筛选。

  2. 计算原理与公式

  核心思路：通过对比 “训练 GNN” 与 “未训练 GNN” 的解释结果相似性 —— 若相似性低，说明解释依赖模型学到的规律（通过检验）；若相似性高，说明解释与模型无关（未通过检验）。

  具体步骤

1. 1. 构建两个对比模型：

      1. 模型 1（训练 GNN）：已在数据集上训练完成、具备良好分类性能的目标 GNN（如 Mutagenicity 上准确率 0.806 的 GIN）；

      2. 模型 2（未训练 GNN）：与模型 1 结构完全一致，但所有参数随机初始化（无任何决策能力，预测接近随机）；

   2. 生成两类解释的边重要性排名：用同一解释方法分别为模型 1 和模型 2 生成同一图实例 $ \mathcal{G} $ 的边重要性分数，再按从高到低排序，得到两个排名列表 $ \Phi(\mathcal{G}, f(\mathcal{G})) $ （训练 GNN）和 $ \Phi(\mathcal{G}, \overline{f}(\mathcal{G})) $ （未训练 GNN）；

   3. 计算等级相关系数：计算两个排名列表的斯皮尔曼等级相关系数 $ \rho $ ，取其绝对值 $ |\rho| $ ；

   4. 求期望得到 SC：对所有图实例求平均，得到最终的合理性检验分数：

      $ SC = \mathbb{E}_{\mathcal{G} \sim \mathbb{G}}[|\rho(\Phi(\mathcal{G}, f(\mathcal{G})), \Phi(\mathcal{G}, \overline{f}(\mathcal{G})))|] $

• • 符号说明： $ f(\mathcal{G}) $ 为训练 GNN 的预测结果， $ \overline{f}(\mathcal{G}) $ 为未训练 GNN 的预测结果，其他符号与 CST 一致。

  3. 结果解读标准

• • SC 值越低越好：
  • 若 $ SC \approx 0 $ ：说明 “训练 GNN 的解释” 与 “未训练 GNN 的解释” 几乎无关，解释依赖模型学到的决策逻辑（如识别分子图中的致癌结构、场景图中的物体关系），通过合理性检验；
  • 若 $ SC \approx 1 $ ：说明两类解释高度相似，解释仅与图的随机特征相关（如优先选择度数高的边），与模型决策无关，属于 “伪解释”，未通过检验。

  4. 实验中 SC 的关键结果（呼应原文）

• • RC-Explainer 安全通过合理性检验，证明其解释依赖目标 GNN 的真实决策：

• • • Mutagenicity（分子图）：SC=0.248（排名第三），远低于 PGM-Explainer（0.597），说明其解释是基于 GIN 学到的 “致癌分子结构规律”，而非分子图的随机边特征；

• • • Visual Genome（场景图）：SC=0.309（排名第二），仅高于 CXPlain（0.266），验证其解释依赖 APPNP 学到的 “场景 - 物体关系映射”（如 “街道” 与 “车 - 路” 关系的关联）；

• • • REDDIT-MULTI-5K（社交网络）：SC=0.465（排名第四），虽高于 GNNExplainer（0.040）等少数基线，但仍低于 Grad-CAM（0.537）、CXPlain（0.696），说明其解释未受未训练 k-GNN 的随机预测干扰。

  5.CST 与 SC 的核心差异对比

对比维度	对比度（CST）	合理性检验分数（SC）
核心评估目标	解释的 “类间区分度”—— 不同类别预测需不同解释	解释的 “模型依赖性”—— 解释需依赖训练 GNN 的决策逻辑
对比对象	同一图实例的 “原类别解释” 与 “置换类别解释”	同一图实例的 “训练 GNN 解释” 与 “未训练 GNN 解释”
结果优化方向	越低越好（类间解释差异越大）	越低越好（解释越依赖训练模型）
核心作用	确保解释能反映模型的类间决策边界	排除 “伪解释”，验证解释的模型关联性
在实验中的意义	证明 RC-Explainer 能为不同类别生成差异化解释	证明 RC-Explainer 的解释基于 GNN 学到的规律，非随机

5.3.4 实验四：时间复杂度评估（衡量解释效率）​

  实验内容​

• • 核心指标：单图解释时间（秒），统计 RC-Explainer 与基线在 3 个数据集上生成解释的平均推理时间，衡量方法的效率。​

• • 实验操作：在相同硬件环境下，分别对测试集中所有图生成解释，记录单图平均耗时。​

  实验结论​

• • RC-Explainer 在中小规模图上效率优势显著：​

• • Mutagenicity（平均边数 30.77）单图耗时 0.68 秒，远快于 GNNExplainer（2.57 秒）、PGM-Explainer（1.19 秒）；​

• • Visual Genome（平均边数 18.04）单图耗时 0.339 秒，仅慢于梯度类方法（SA：0.015 秒、Grad-CAM：0.015 秒），快于其他基线；​

• • 大规模图（REDDIT-MULTI-5K，平均边数 594.87）耗时 23.8 秒，虽慢于梯度类和 PGExplainer，但远快于 CXPlain（13.4 秒）、PGM-Explainer（64.2 秒），主要因大图动作空间大导致，后续可通过剪枝优化。​

5.3.5 实验五：可视化验证（直观验证解释合理性）​

  实验内容​

• • 实验操作：选取 Mutagenicity（分子图）和 Visual Genome（场景图）的典型实例，可视化 RC-Explainer 与基线生成的解释性子图（突出显示 Top20% 重要边），对比关键边的捕捉能力。​

  实验结论​

• • RC-Explainer 能精准捕捉因果关键边：​

• • • 分子图（致癌预测）：RC-Explainer 可同时捕捉两个硝基的 N=O 键（形成致癌关键联盟），而基线（如 SA、GNNExplainer）仅能捕捉 1 条 N=O 键或误选 N-C 等虚假关联边；​

• • • 场景图（街道预测）：RC-Explainer 优先选择 “车 - 在 - 路”“货车 - 在 - 街道” 等因果边，基线（如 PGM-Explainer）易关注 “树 - 在 - 街道” 等冗余边；​

• • • 失败案例：当选择比例超过 10%（如 μ=0.2）时，RC-Explainer 可能添加与已选边不连通的冗余边（如场景图中 “灯 - 在 - 路”），导致子图偏离原分布（OOD 问题），轻微降低预测准确率。​

5.4 实验整体总结​

  RC-Explainer 在 3 个数据集、多维度评估中均展现出显著优势：​

1. 1. 解释质量：预测准确率（忠实性）、对比度（类间区分度）均优于或 comparable 于当前最先进方法，可视化验证证明其能捕捉真实因果边与协同联盟；​

   2. 可靠性：通过合理性检验，解释依赖 GNN 真实决策逻辑，而非随机特征；​

   3. 效率：中小规模图上效率远超掩码类、扰动类基线，大规模图效率仍有优化空间；​

   4. 局限：大规模图动作空间大、OOD 子图可能影响因果评估，需后续通过动作剪枝、反事实生成解决。