Torch核心数据结构Tensor（张量）

1 基本概念

tensor是一个多维数组，类似于NumPy中的ndarray，但tensor可以在GPU上进行高效计算，这是它与ndarray的重要区别之一。它可以表示标量（0维张量）、向量（1维张量）、矩阵（2维张量）以及更高维度的张量，广泛应用于表示模型的输入、输出、参数等。下图比较形象的给出了各种张良：

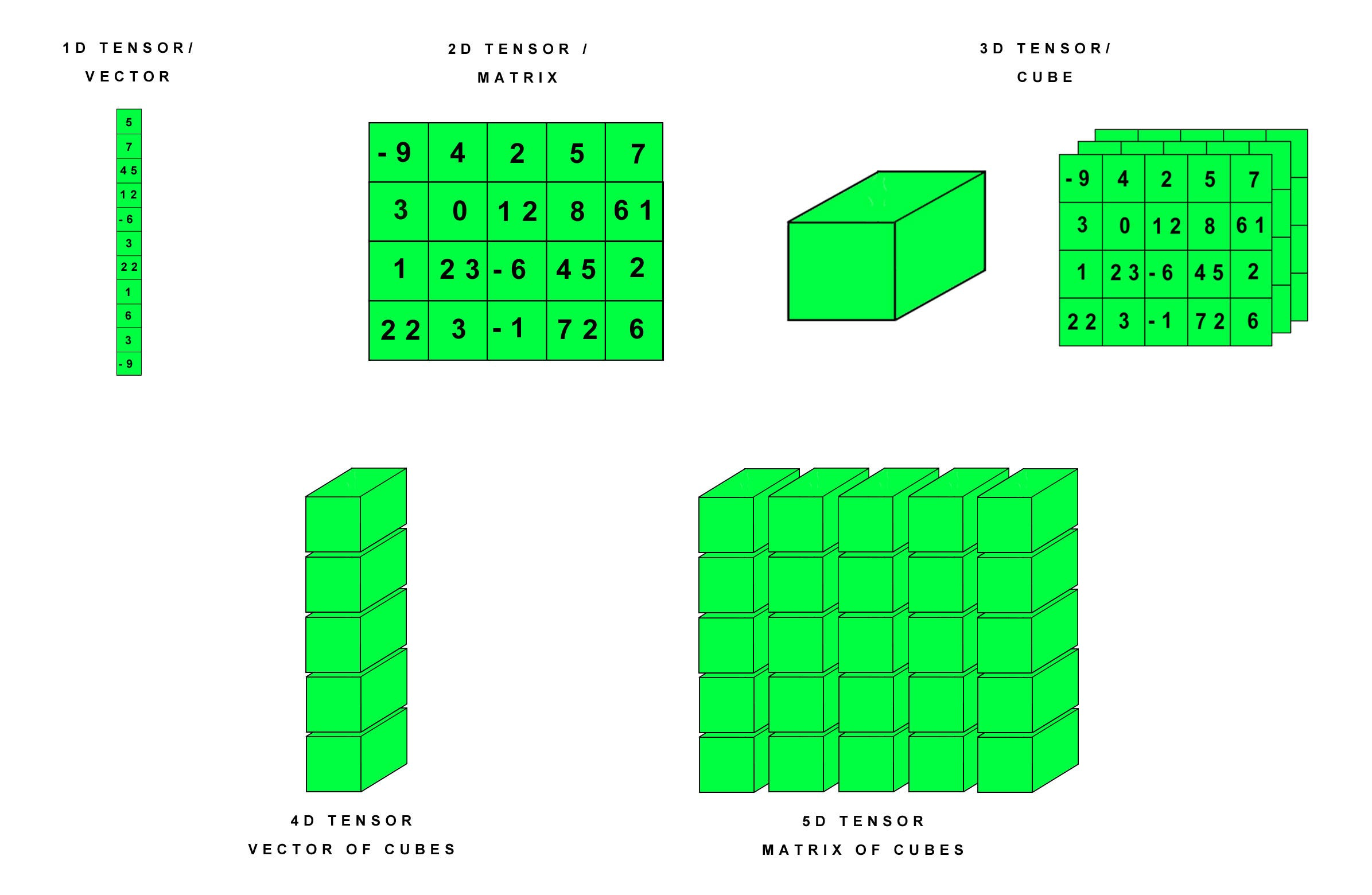
1.1 创建方式

1. 直接创建

通过torch.tensor()函数，可以直接从python列表或NumPy数组创建张量：

import torch
import numpy as np# 从Python列表创建张量
data = [1, 2, 3]
x = torch.tensor(data)# 从NumPy数组创建张量
arr = np.array([4, 5, 6])
y = torch.tensor(arr)

2. 使用特定函数创建

torch.zeros()：创建全 0 张量。例如，torch.zeros((3, 4))会创建一个形状为(3, 4)（3 行 4 列）的全0矩阵。

torch.ones()：创建全 1 张量。例如，torch.ones((2, 2))会生成一个2x2的全1矩阵。

torch.rand()：创建一个由在区间[0, 1)上均匀分布的随机数填充的张量。比如torch.rand((2, 3))会得到一个2行3列的随机数张量。

torch.arange()：类似于 Python 的range()函数，创建一个等差序列的张量。例如torch.arange(0, 10, 2)会生成tensor([0, 2, 4, 6, 8])。

import torchzero_tensor = torch.zeros((3, 4))
print("zero_tensor:\n", zero_tensor)ones_tensor = torch.ones((2, 2))
print("ones_tensor:\n", ones_tensor)rand_tensor = torch.rand((2, 3))
print("rand_tensor:\n", rand_tensor)arange_tensor = torch.arange(0, 10, 2)
print("arange_tensor:\n", arange_tensor)

1.2 张量属性

形状（shape）：通过.shape属性获取张量的形状，例如对于x = torch.tensor([[1, 2], [3, 4]])，x.shape返回torch.Size([2, 2]) ，表示这是一个 2 行 2 列的张量。

数据类型（dtype）：通过.dtype属性获取张量的数据类型，常见的数据类型包括torch.float32、torch.int64、torch.bool等。创建张量时也可以指定数据类型，如torch.tensor([1, 2, 3], dtype=torch.float32)。

设备（device）：通过.device属性获取张量所在的设备，是在CPU还是在GPU上。可以通过.to()方法将张量移动到不同设备，如x = x.to('cuda')（前提是系统支持CUDA且安装了相关驱动）将张量x移动到GPU上进行计算。

requires_grad：该属性是张量的核心属性，用于控制是否追踪该张量的计算历史并计算梯度，是实现自动微分（Automatic Differentiation）的关键开关，如果requires_grad为True，则会为张量分配grad属性，用于存储其梯度。

is_cuda：是一个布尔属性，用来判断一个张量是否在 GPU（CUDA 设备） 上。

1.3 张量操作

索引和切片：与 Python 列表和 NumPy 数组类似，张量可以进行索引和切片操作。例如对于x = torch.tensor([[1, 2, 3], [4, 5, 6]])，x[0, 1]返回第一行第二列的元素2；x[:, 1]返回第二列的所有元素。

数学运算：支持各种数学运算，如加法、减法、乘法、除法等。既可以是张量与标量的运算，也可以是张量与张量之间的运算。例如x + 2表示张量x的每个元素都加 2；x + y（x和y是形状相同的张量）表示对应元素相加。

维度操作：torch.unsqueeze(input, dim)增加维度，例如x形状为Size([3])，则torch.unsqueeze(x, 0)会在索引为0的位置上增加一个维度，形状变为Size([1, 3])，而torch.unsqueeze(x, 1)会在索引为1的位置上增加一个维度，形状变为Size([3, 1])，这里dim参数的取值范围为[-n, n-1]（n是原始张量的维度数），非负数索引时，dim=0对应最外层维度，dim=1对应次外层维度，负数索引时，dim=-1对应最内层维度，dim=-2对应次内层维度，以此类推；torch.squeeze(input, dim=None)，当不指定dim时，删除张量中所有大小为1的维度，当指定dim时，仅删除第dim个维度（前提是该维度的大小为1，否则不做任何改变）；torch.transpose(input, dim0, dim1)，转置张量，即交换张量中指定的两个维度，而保持其他维度的顺序不变；torch.reshape(input, shape)，改变张量的形状，如对于形状为Size([3, 2])（3行2列）的x，torch.reshape(x, (2, 3))将张量x重塑为2行3列的形状。分析可知，以上操作都是在不改变张量元素数据及总数的前提下，重新组织张量的维度结构。

1.4 张量方法

其实对于相应的张量操作，张量自身都有对应的方法。

1. 索引与切片

index_select(dim, index)

按索引在指定维度上选择元素，示例代码如下：

import torchx = torch.tensor([[1,2],[3,4],[5,6]])
idx = torch.tensor([0,2])
print(x.index_select(0, idx))  # 选择第0和第2行，输出tensor([[1, 2], [5, 6]])

masked_select(mask)

根据布尔掩码选择元素（返回1D张量），示例代码如下：

import torchx = torch.tensor([[1,5],[3,4]])
mask = x > 2
x.masked_select(mask)       # 输出tensor([5, 3, 4])

gather(dim, index)

沿指定维度收集元素（更灵活的索引方式），该函数的核心逻辑：沿指定维度（dim），根据索引张量（index）收集输入张量（x）中的元素，输出张量的形状与索引张量（index）的形状完全一致，所以这里idx必须满足维度和x相同，但是每个维度上元素个数不大于x相应维度上元素个数。

import torchx = torch.tensor([[[1,5], [2, 6]], [[3,7], [4,8]]])
idx=torch.tensor([[[1]],[[0]]])
print(x.gather(2, idx))
print(x.gather(1, idx)) 
print(x.gather(0, idx))

代码中，x形状为 (2, 2, 2)，即：dim=0（第 1 维），dim=1（第 2 维），dim=2（第 3 维）大小都为 2。

idx形状为(2, 1, 1)，即dim=0为2，dim=1和dim=2都为1，其内容为：

idx[0,0,0] = 1  # 第0行、第0列、第0深的索引值
idx[1,0,0] = 0  # 第1行、第0列、第0深的索引值

gather的核心逻辑是，对于输出张量的每个位置 (i,j,k)，其值由以下规则确定：
output[i,j,k] = x[i,j,k] 中，将参数dim维度的索引替换为 idx[i,j,k]，即：
若 dim=0：output[i,j,k] = x[ idx[i,j,k], j, k ]
若 dim=1：output[i,j,k] = x[ i, idx[i,j,k], k ]
若 dim=2：output[i,j,k] = x[ i, j, idx[i,j,k] ]

以x.gather(2, idx)（沿dim=2收集）为例，dim=2是 “深维度”（最内层维度），规则：output[i,j,k] = x[i,j, idx[i,j,k]]，输出形状与idx一致(2,1,1)，具体计算：

i=0, j=0, k=0：idx[0,0,0]=1 → output[0, 0, 0] = x[0,0,1] = 5（第 0 行、第 0 列、第 1 深的值）

i=1, j=0, k=0：idx[1,0,0]=0 → output[1, 0, 0] = x[1,0,0] = 3（第 1 行、第 0 列、第 0 深的值）

结果：tensor([[[5]], [[3]]])。

同理，对于x.gather(1, idx)（沿dim=1收集），dim=1是“列维度”（中间维度），规则：output[i,j,k] = x[i, idx[i,j,k], k]。输出形状为(2,1,1)，具体计算：

i=0, j=0, k=0：idx[0,0,0]=1 → output[0, 0, 0] = x[0,1,0] = 2（第 0 批次、第 1 行、第 0 列的值）

i=1, j=0, k=0：idx[1,0,0]=0 → output[1, 0, 0] = x[1,0,0] = 3（第 1 批次、第 0 行、第 0 列的值）

结果：tensor([[[2]], [[3]]])。

最后，x.gather(0, idx)（沿dim=0收集），dim=0是 “行维度”（最外层维度），规则：output[i,j,k] = x[ idx[i,j,k], j, k ]。输出形状为(2,1,1)，具体计算：

i=0, j=0, k=0：idx[0,0,0]=1 → output[0, 0, 0] = x[1,0,0] = 3（第 1 行、第 0 列、第 0 深的值）

i=1, j=0, k=0：idx[1,0,0]=0 → output[1, 0, 0] = x[0,0,0] = 1（第 0 行、第 0 列、第 0 深的值）

结果：tensor([[[3]], [[1]]])。

一下代码可以直观的给出张量x立体示意图：

import torch
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D# 设置中文字体
plt.rcParams["font.family"] = ["SimHei", "WenQuanYi Micro Hei", "Heiti TC"]
# 解决负号显示问题（可选）
plt.rcParams['axes.unicode_minus'] = False  # 正确显示负号# 创建张量
x = torch.tensor([[[1,5], [2, 6]], [[3,7], [4,8]]])# 转换为numpy数组以便绘图
x_np = x.numpy()# 创建3D图形
fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111, projection='3d')# 获取张量的维度
depth, rows, cols = x_np.shape# 创建坐标网格
x_coords, y_coords, z_coords = np.meshgrid(np.arange(rows), np.arange(cols), np.arange(depth), indexing='ij')# 展平坐标和值
x_flat = x_coords.flatten()
y_flat = y_coords.flatten()
z_flat = z_coords.flatten()
values = x_np.flatten()# 绘制点
scatter = ax.scatter(x_flat, y_flat, z_flat, c=values, s=500, cmap='viridis', alpha=0.8)# 添加标签
for i, (x, y, z, val) in enumerate(zip(x_flat, y_flat, z_flat, values)):ax.text(x, y, z, f'{val}', fontsize=12, ha='center', va='center', color='white')# 设置坐标轴标签
ax.set_xlabel('行 (Row)')
ax.set_ylabel('列 (Column)')
ax.set_zlabel('深度 (Depth)')# 设置坐标轴刻度
ax.set_xticks(np.arange(rows))
ax.set_yticks(np.arange(cols))
ax.set_zticks(np.arange(depth))# 添加标题
ax.set_title('3D张量可视化\n形状: {}'.format(x_np.shape))# 添加颜色条
cbar = fig.colorbar(scatter, ax=ax, shrink=0.5, aspect=20)
cbar.set_label('元素值')# 设置视角以便更好地观察
ax.view_init(elev=20, azim=45)plt.tight_layout()
plt.show()

代码运行后如下所示：

2. 数学运算

x.add(y)：对应元素相加

x.sub(y)：对应元素相减

x.mul(y)：对应元素相乘

x.div(y)：对应元素相除

x.remainder(y)：对应元素取余

x.pow(y)：对x每个元素求y次幂

x.sqrt()：对x每个元素求平方根

x.exp()：对x每个元素求自然指数（e^x）

x.mean()：求平均值，要求x数据类型为float或者complex

x.sum()：求和

x.max()/x.min()：求最大/最小值

x.std()/var()：求标准差/方差，要求x数据类型为float或者complex

3. 维度相关

该部分方法对应维度操作部分，不再详细介绍。

4. 内存与类型

contiguous()

将张量转为内存连续的形式（用于view等方法前），以张量x = torch.tensor([[1, 2, 3], [4, 5, 6]])为例，它是contiguous意味着沿第0维（行）移动1步，需跳过3个元素；沿第1维（列）移动1步，需跳过1个元素。当张量经过某些维度操作（如 transpose、permute、unsqueeze/squeeze 等）后，可能会变成非连续张量（内存中元素的存储顺序与逻辑顺序不一致）。此时，若调用某些要求张量连续的操作（如 view、resize_ 等），会抛出错误，这种情况下就需要调用contiguous()进行转换。

to(dtype)

转换张量数据类型（如float32→float64）。

cpu()/cuda()

将张量转移到 CPU 或 GPU（需 CUDA 支持）。

5. 原地操作

多数方法有后缀_的原地版本（直接修改自身，不返回新张量），如x.add_(3)等价于 x = x + 3。

6. 其他方法

clone()：创建张量的副本（深拷贝，不共享内存）。

detach()：返回与原张量共享数据，但不关联计算图的张量（用于冻结参数）。

numpy()：将张量转为 NumPy 数组（CPU 张量适用，共享内存）。

flatten(start_dim=0, end_dim=-1)：展平指定范围的维度。

2 张量自动求导（Autograd）

autograd是实现自动微分（Automatic Differentiation） 的核心系统，它能自动计算张量的梯度，是训练神经网络的基础。

2.1 核心概念

1. 计算图（Computational Graph）

PyTorch在执行张量运算时，会动态构建一张有向无环图 (DAG)：

• 节点 (Node)：张量（数据）

• 边 (Edge)：操作 (Operation, Function)

例如：

import torch
x = torch.tensor(2.0, requires_grad=True)
y = x**2 + 3*x + 1　　　　　　　　# 向前传播，会创建计算图

其计算过程可以分解为：

1）a = x**2 (平方运算)

2）b = 3*x (乘法运算)

3）c = a + b (加法运算)

4）y = c + 1 (加法运算)

则其对应的计算图DAG可表示如下：

    x (requires_grad=True)│├─── PowBackward (2) ─── a = x²│└─── MulBackward (3) ─── b = 3*x││a       b\     /AddBackward ─── c = a + b││  1│ /AddBackward ─── y = c + 1

叶子节点

x：初始张量，requeires_grad = True，梯度计算起点。

中间节点

PowBackward：x**2 操作，记录幂运算的梯度计算规则

MulBackward：3*x 操作，记录标量乘法的梯度计算规则

AddBackward (1)：a + b 操作，记录加法的梯度计算规则

AddBackward (2)：c + 1 操作（常数1不参与梯度计算）

2. 前向传播（Forward Pass）

在该过程中会创建计算图，同时，计算运算的输出张量，记录运算的元信息（如运算类型、输入张量、梯度函数），用于后续反向传播，以上代码中第3行就是前向传播。

3. 反向传播 (Backward Pass)

而在反向传播中，tensor variable需要缓存原来的tensor来计算反向传播梯度，如果想要计算各个variable的梯度，只需调用根节点variable的backward方法，autograd会自动沿着计算图反向传播，计算每一个叶子节点的梯度。

tensor.backward(gradient=None, retain_graph=None, create_graph=False, inputs=None)

主要有如下参数：

gradient：梯度初始值，当根节点是标量时，gradient可省略，当根节点是高维张量时，形状与variable一致，对于y.backward()。

retain_graph：是否保留计算图（支持多次反向传播），通常反向传播以后，计算图等相关中间结果会被释放清空，通过该参数可指定不清空，以用来多次反向传播。即复用已保留的计算图，再次计算梯度，新梯度与已有梯度累加。

create_graph：是否创建梯度的计算图（支持高阶导数），当该参数为False时，仅计算梯度值，不记录梯度的计算过程，无法对梯度再求导，当为True时，会构建梯度的计算图，允许对梯度进行二次求导（二阶导数）、三次求导（三阶导数）等高阶导数计算。

inputs：指定需要计算梯度的叶子节点（优化计算效率）。

当调用 y.backward() 时，会从输出张量y开始，沿计算图反向遍历，依次调用各操作的链式法则，最终把梯度累积到x.grad里。

y → AddBackward(2) → AddBackward(1) → ├── (常数1，无梯度)└── c → AddBackward(1) → ├── a → PowBackward → x└── b → MulBackward → x

根据链式法则，有：

∂y/∂x = ∂y/∂c * ∂c/∂x= ∂y/∂c * ∂c/∂a * ∂a/∂x + ∂y/∂c * ∂c/∂b * ∂b/∂x= 1 * 1 * (2x) + 1 * 1 * 3= 2*2 + 3 = 7

可以在之前的代码中增加验证：

y.backward()　　 # 计算图在backward()后被销毁（除非retain_graph=True）
print(x.grad)   # 输出: tensor(7.)

需要说明的是：DAG在PyTorch中是动态构建的，每次前向传播都会重新创建，但在反向传播后会被自动销毁（除非指定retain_graph=True）。

2.2 关键机制与特性

1. 动态计算图（Dynamic Graph）

PyTorch的计算图是动态构建的：每次前向传播都会重新构建计算图，支持在运行时根据条件（如if、for）修改图结构，使得调试和修改模型变得更加容易。与TensorFlow 1.x 的静态图（计算图在开始执行之前构建完成，并且不会改变）不同，更灵活且易于调试，新版本的TensorFlow也已经支持动态图。

import torchx = torch.tensor(1.0, requires_grad=True)
for i in range(3):y = x * 2if i % 2 == 0:y = x * 3  # 条件分支修改计算图
    y.backward()print(x.grad)  # 每次反向传播后梯度累积x.grad.zero_()  # 清零梯度，避免累积

以上程序输出：

tensor(3.)
tensor(2.)
tensor(3.)

2. 梯度累积与清零

多次调用backward()会累积梯度（适用于大 batch 拆分训练），需通过.grad.zero_()手动清零梯度（否则会影响下一轮计算）。

3. 非叶子节点的梯度释放

中间节点（非叶子节点）的梯度在反向传播后会被自动释放，以节省内存。若需保留，可使用retain_grad()方法：

import torchx = torch.tensor(1.0, requires_grad=True)
y = x * 4
y.retain_grad()  # 保留y的梯度
z = y * 2
z.backward()
print(y.grad)  # 输出：tensor(1.) → dz/dy = 1
print(x.grad)

以上代码能正确输出结果，但是如果将y.retain_grad()这行注释掉，则会提示一下错误：

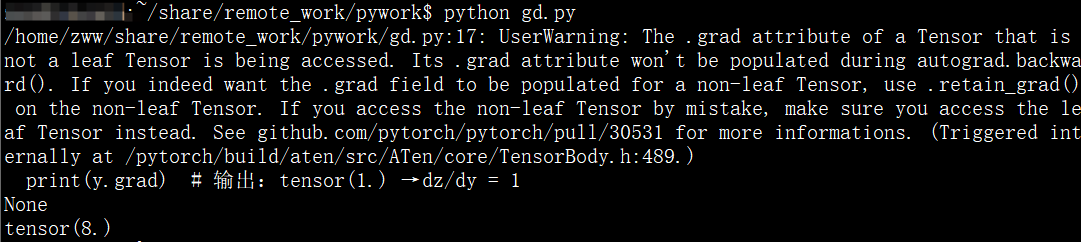
4. detach()方法

tensor.detach()会返回一个与原张量数据相同，但requires_grad=False的新张量，且脱离计算图，不再参与梯度传播：

x = torch.tensor(2.0, requires_grad=True)
y = x.detach()  # y.requires_grad=False，与计算图分离
z = y * 3
z.backward()  # 报错：z不依赖任何requires_grad=True的张量

2.3 Function类：梯度计算的核心

autograd的梯度计算依赖Function类，每个运算（如加法、乘法）都对应一个Function子类，其中：

forward()方法：定义前向传播的计算逻辑；

backward()方法：定义反向传播的梯度计算逻辑（即局部梯度）。

当执行y = x * w时，autograd会隐式创建一个MulBackward（乘法对应的Function）实例，记录输入x、w，并在反向传播时调用其backward()方法计算梯度。

目前绝大多数函数都可以使用autograd实现反向求导，但如果需要自己写一个复杂的函数，不支持自动反向求导时，这时需写一个Function，实现它的前向传播和反向传播代码，示例代码如下：

import torch
from torch.autograd import Functionclass MultiplyAdd(Function):                                 @staticmethoddef forward(ctx, w, x, b):                              ctx.save_for_backward(w,x)output = w * x + breturn output@staticmethoddef backward(ctx, grad_output):                         w,x = ctx.saved_tensorsgrad_w = grad_output * xgrad_x = grad_output * wgrad_b = grad_output * 1return grad_w, grad_x, grad_b                       x = torch.ones(1)
w = torch.rand(1, requires_grad = True)
b = torch.rand(1, requires_grad = True)
print(x, w, b)
# 开始前向传播
z=MultiplyAdd.apply(w, x, b)
# 开始反向传播
z.backward()# x不需要求导，中间过程还是会计算它的导数，但随后被清空
print(x.grad, w.grad, b.grad)

分析如下：

1. 自定义的Function需要继承autograd.Function，没有构造函数__init__，forward和backward函数都是静态方法；

2. backward函数的输出和forward函数的输入一一对应，backward函数的输入和forward函数的输出一一对应；

3. backward函数的grad_output参数即torch.autograd.backward中的gradient，w的梯度grad_w是上游梯度grad_output乘以 x（对w求导，d(output)/dw = x)；求x的梯度grad_x，根据 x 是否需要求导（ctx.x_requires_grad），若需要，grad_x = grad_output * w（对 x 求导，d(output)/dx = w）；否则为 None，上述实例中requires_grad默认为False，所以x梯度输出是None；对于b的梯度，grad_b = grad_output * 1，b 的梯度是上游梯度乘以 1（对 b 求导，d(output)/db = 1）；

4. 如果某一个输入不需要求导，直接返回None，如forward中的输入参数x_requires_grad显然无法对它求导，直接返回None即可；

5. 反向传播可能需要利用前向传播的某些中间结果，需要进行保存，否则前向传播结束后这些对象即被释放。

 

参考

1. https://www.runoob.com/pytorch/pytorch-basic.html

2. https://blog.csdn.net/qq_43328040/article/details/108421469